Schwingende Kurbelschleife und Viergelenkkette

Mit interaktiven Animationen (es können alle Abmessungen modifiziert werden) für die schwingende Kurbelschleife (links) und die allgemeine Viergelenkkette (rechts) können mannigfalige Bewegungen und Bahnkurven für Koppelpunkte erzeugt werden.

Viergelenkketten

Spezielle Bahnkurven eines Punktes werden erzeugt durch Kurbelschwinge und Doppelschwinge (oben), Doppelkurbeln und die geniale Kopplung zweier Kurbelschwingen zum "Strandbeest-Mechanismus" von Theo Jansen (unten rechts).

Krümmungskreise an eine Bahnkurve

In die Berechnung der Normalbeschleunigung der Bewegung eines Punktes geht der Krümmungsradius der Bahnkurve ein, der sich ständig ändert. Die Animation demonstriert dies, indem für den jeweils aktuellen Punkt der (roten) Bahnkurve der (blaue) Krümmungskreis gezeichnet wird.

Kinematik starrer Körper

Unter diesem Text sieht man eine Kurbelschwinge, darunter eine "Schwingende Kurbelschleife". Das Malteserkreuz in der Mitte und die Kurbelschleife (Gabelschwinge) darunter bewegen sich nach den gleichen kinematischen Gesetzen. Rechts sieht man eine "Exzentrische Schubkurbel".

Links sieht man zwei Varianten des so genannten Doppelschiebers.

Unten ist eine zentrische Schubkurbel zu sehen, bei der die Kurbel mit konstanter Winkelgeschwindigkeit über das Pleuel den Gleitstein antreibt, dessen sich ändernde Geschwindigkeit durch den gelben Pfeil angedeutet wird.

Einfaches Planetengetriebe

Der (rote) Steg rotiert mit konstanter Drehzahl und nimmt das (hellblaue) Planetenrad mit. Dieses rollt (linkes Bild) auf dem innenverzahnten (grau/weißen) Gehäuse und nimmt das (blaue) Sonnenrad mit. Im rechten Bild ist das gleiche Getriebe zu sehen, bei dem außerdem das (grau/weiße) Gehäuse (mit entgegengesetztem Drehsinn) rotiert. Das Planetenrad treibt dadurch das (blaue) Sonnenrad zu einer Rotation mit größerer Drehzahl.

Planetengetriebe mit zwei Planetenrädern

Der (rote) Steg rotiert mit konstanter Drehzahl und nimmt zwei Planetenräder mit. Das äußere Planetenrad rollt (linkes Bild) auf dem innenverzahnten (grau/weißen) Gehäuse, treibt das innere Planetenrad und dieses das Sonnenrad, das mit zum Steg entgegengesetzter Drehrichtung rotiert. Im rechten Bild ist das gleiche Getriebe zu sehen, bei dem außerdem das (grau/weiße) Gehäuse (mit zum Steg entgegengesetztem Drehsinn) rotiert. Das Planetenrad treibt dadurch das (blaue) Sonnenrad zu einer Rotation mit größerer Drehzahl.

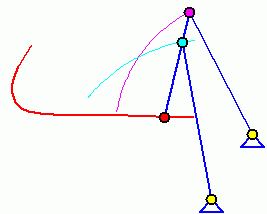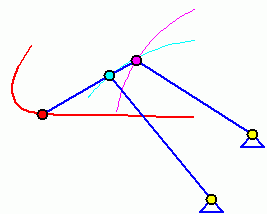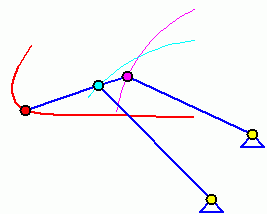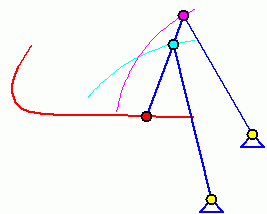
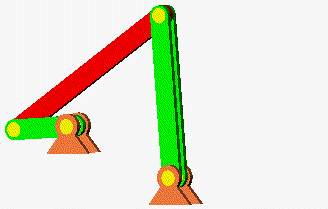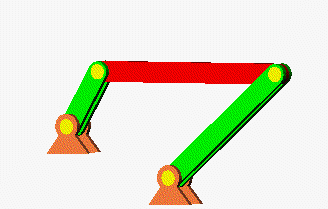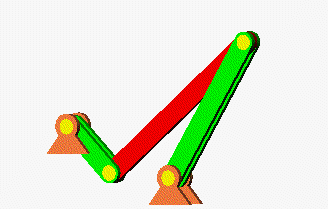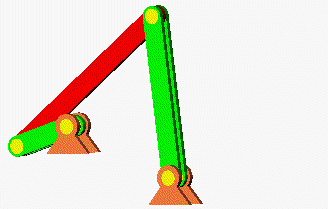
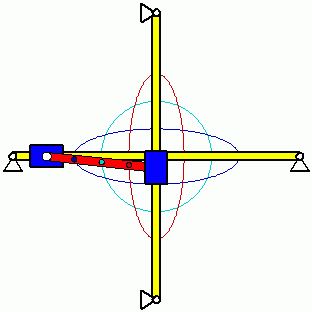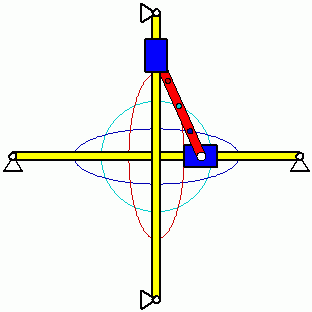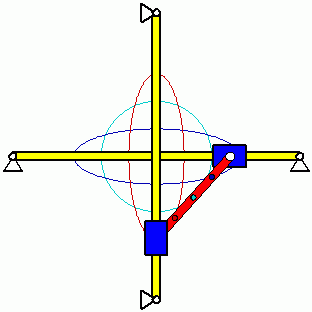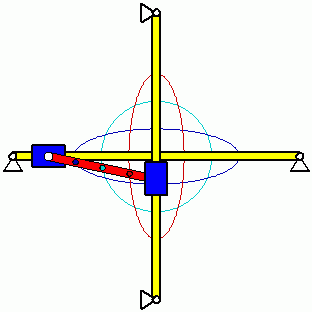
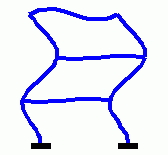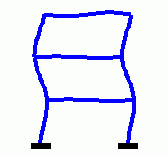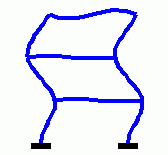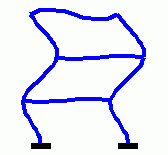
Eigenschwingungen eines biege- und dehnsteifen Rahmens

Die drei Bilder zeigen die zu den kleinsten drei Eigenfrequenzen des Rahmens gehörenden Schwingungsformen.

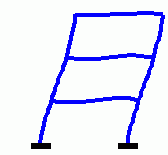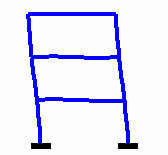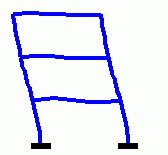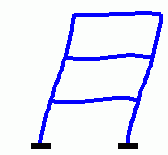
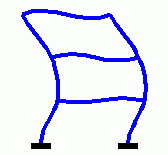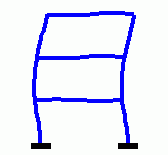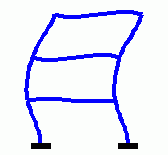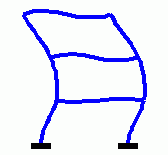
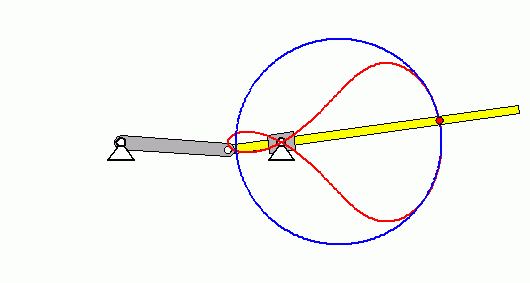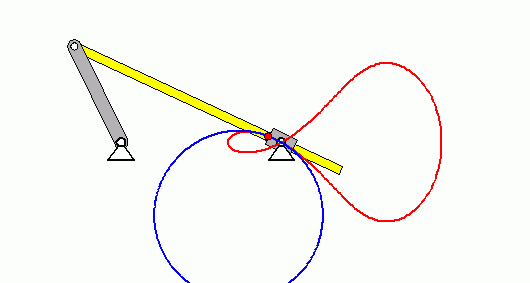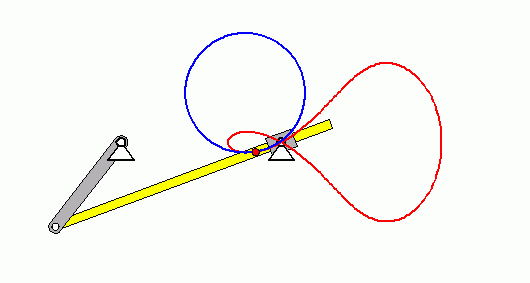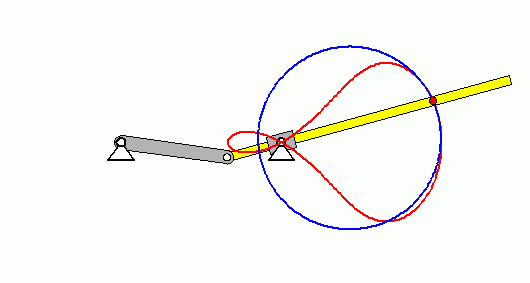
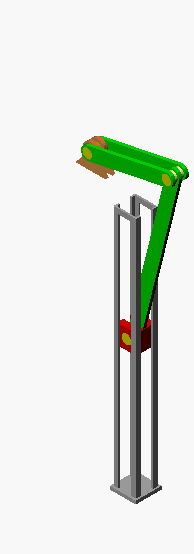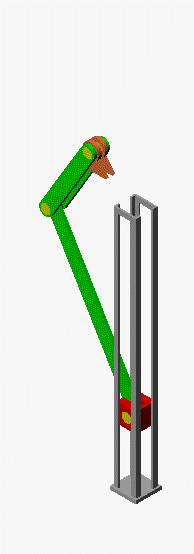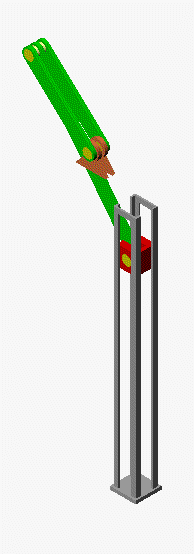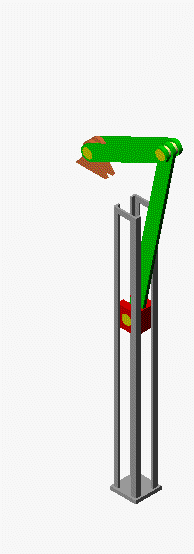
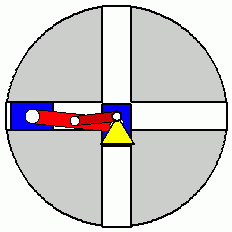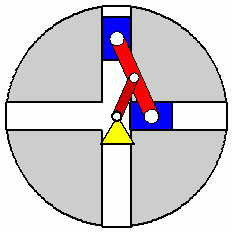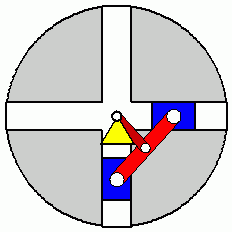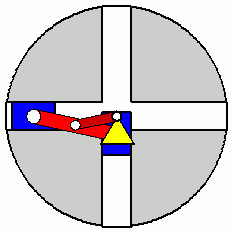
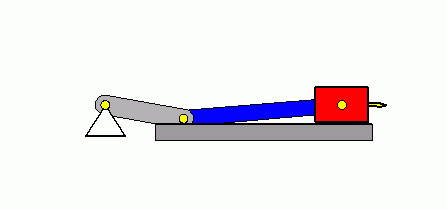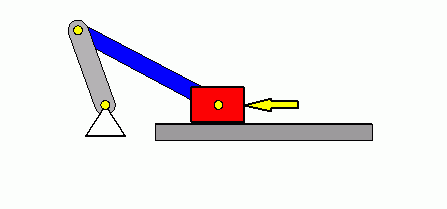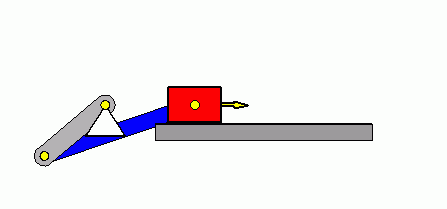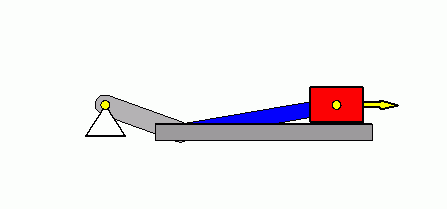
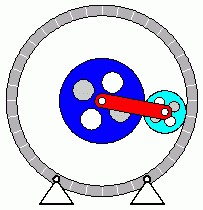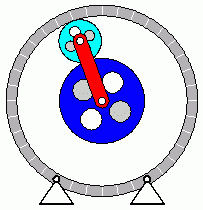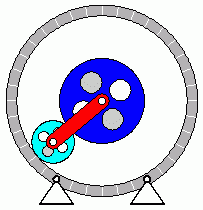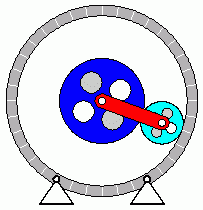
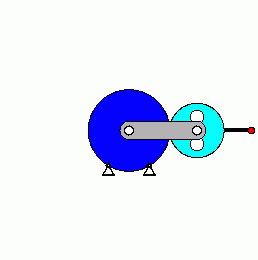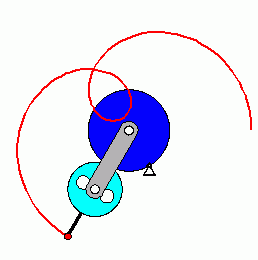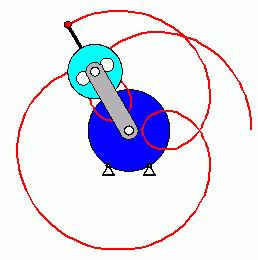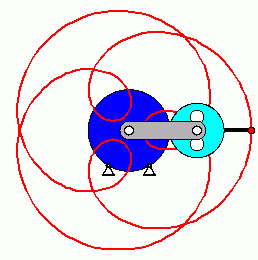
Verifizieren der Lösungen von Anfangswertproblemen

Komplizierte Bewegungsvorgänge, die durch die Lösungen von nichtlinearen Angangswertproblemen beschrieben werden, sind schwierig zu verifizieren. Eine Animation gibt immerhin ein "Gefühl" dafür, ob das Ergebnis plausibel ist (auf die Bilder klicken, um zur Behandlung des zugehörigen Anfangswertproblems zu kommen).

Das frei schwingende Doppelpendel rechts und die Laufkatze, die kurzzeitig angetrieben und dann sich selbst überlassen wird (mittlere Zeile links), sind Systeme mit zwei Freiheitsgraden. Speziell die chaotische Bewegung eines Doppelpendels ist nur kurzzeitig zu simulieren. Ein "Dauerläufer" (kleines Bild) ist immer "geschummelt", der darunter (größeres Bild) dargestellten Bewegung über etwa 10 Sekunden darf man vertrauen. Unten links sieht man die freie Schwingung eines Doppelschiebers, daneben ein weiteres Schwingungssystem mit einem Freiheitsgrad (Walze auf schiefer Ebene).

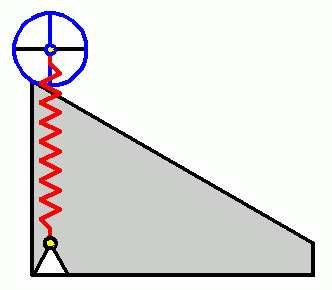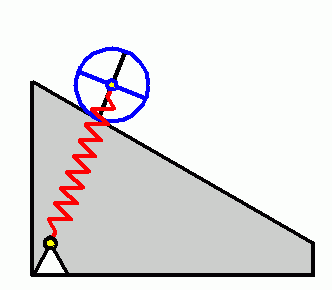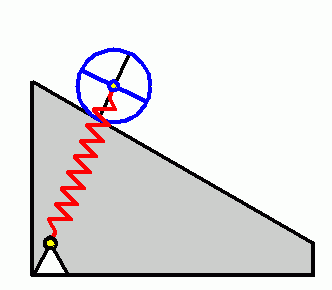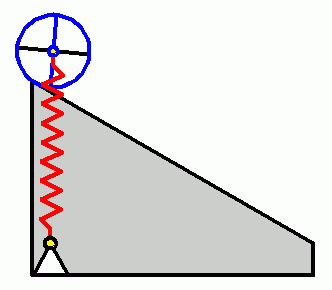
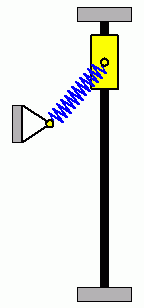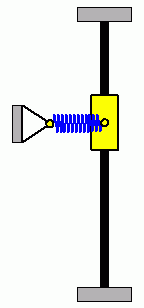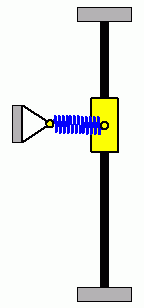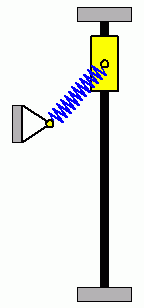
Die beiden nebenstehenden Animationen verdeutlichen ein typisches Problem nichtlinearer Anfangswertaufgaben. Die beiden System haben identische Parameter, beide Gleitsteine starten mit Anfangsauslenkungen nach oben (ohne Anfangsgeschwindigkeiten), die sich so minimal unterscheiden, dass die Unterschiede nicht zu erkennen sind.

Der linke Gleitstein mit der geringfügig größeren Anfangsauslenkung schafft es am Punkt der größten Zusammendrückung der Feder, sich gerade noch "vorbeizudrängeln", der rechte Gleitstein schafft das nicht, und so ergeben sich völlig unterschiedliche Bewegungsabläufe.

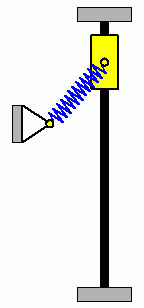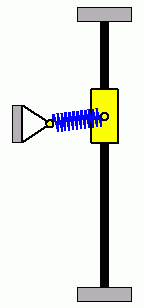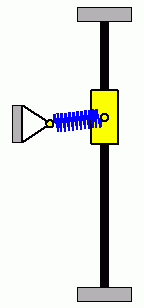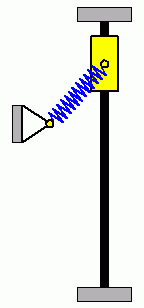
Bewegung eines Punktes eines rollenden Rades

Ein Punkt auf einem rollenden Rad bewegt sich relativ zum ruhenden System auf einer Zykloide, wenn das Rad auf einer Geraden rollt. Wenn der Punkt auf der Peripherie des rollenden Rades liegt, entsteht eine "Spitze Zykloide", wenn sein Abstand vom Mittelpunkt des rollenden Rades kleiner als dessen Radius ist, entsteht eine "Verkürzte Zykloide", ist dieser Abstand größer als der Radius, entsteht eine verlängerte Zykloide.

Nachfolgend sieht man drei Epizykloiden, rechts unten eine Hypozykloide. Bei Epizykloiden rollt ein Kreis (Planetenrad) auf einem feststehenden anderen Kreis (Sonnenrad) ab. Ist der Abstand des Punktes, dessen Bahnkurve verfolgt wird, vom Mittelpunkt des rollenden Kreises größer als dessen Radius, entstehen "Verlängerte Epizykloiden" (die beiden Bilder in der oberen Reihe). Wenn das Verhältnis "Sonnenradradius/Planetenradradius" ganzzahlig ist (die beiden Bilder links), schließt sich die Bahnkurve bereits nach einem Umlauf, ansonsten (rechtes Bild) werden mehrere Umläufe (hier: 2) benötigt.

Unten rechts sieht man eine "Spitze Hypozykloide" (Kreis rollt innen in einem anderen Kreis mit doppeltem Radius).