
Aufgabe
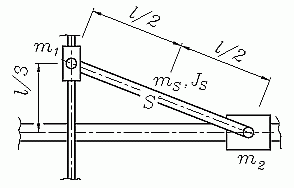
Zwei Massen m1 und m2 können auf einer vertikalen bzw. einer horizontalen Führung reibungsfrei gleiten. Sie sind durch eine starre Stange (Masse mS und Massenträgheitsmoment JS bezüglich des Schwerpunktes S) gekoppelt. Das gesamte System wird aus der skizzierten Lage ohne Anfangsgeschwindigkeit freigelassen. Für den Bewegungsvorgang sollen die Kräfte in den Bolzen berechnet werden, die die Massen mit der Stange verbinden.
Gegeben:
Bewegungs-Differenzialgleichung, Bolzenkräfte
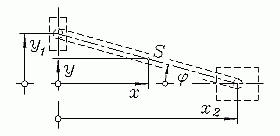
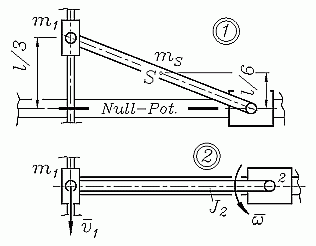
Während sich die Massen m1 und m2 rein translatorisch bewegen, führt die Stange eine allgemeine ebene Bewegung aus. Die nebenstehende Abbildung zeigt die gewählten Koordinaten: Der Schwerpunkt der Stange wird durch x und y verfolgt, die Drehung der Stange durch den Winkel φ, für die beiden Massen wurden die Koordinaten y1 bzw. x2 definiert.
Das System hat nur einen Freiheitsgrad, deshalb können aus relativ einfachen geometrischen Zusammenhängen folgende Zwangsbedingungen formuliert werden:
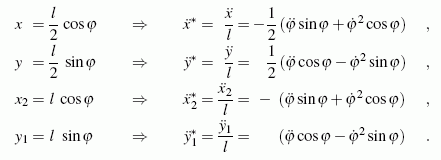
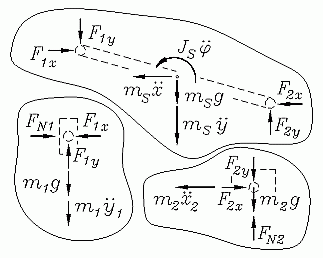
Nebenstehend sieht man das freigeschnittene System, an dem die Gleichgewichtsbedingungen formuliert werden können. Vier Kraftgleichgewichtsbedingungen (an den Massen je eine, an der Stange zwei) können nach den Komponenten der Bolzenkräfte umgestellt werden, die in dimensionsloser Form aufgeschrieben werden:
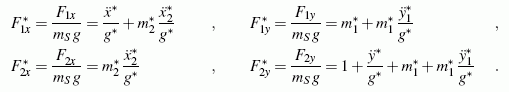
Berechnet werden können diese Bolzenkraftkomponenten natürlich erst dann, wenn die Beschleunigungen, die in allen Formeln auftauchen, bekannt sind. Weil mit den oben angegebenen Zwangsbedingungen alle Beschleunigungen durch eine ausgedrückt werden können, fehlt noch eine Gleichung. Dafür steht noch das Momentengleichgewicht an der Verbindungsstange zur Verfügung. Im Kapitel "Kinetik starrer Körper" wird gezeigt, dass man in dieser Gleichgewichtsbedingung alle Kräfte entsprechend den oben angegebenen Formeln ersetzen kann und schließlich alle Beschleunigungen mit Hilfe der Zwangsbedingungen durch eine ersetzen kann. Auf diese Weise kommt man zur Bewegungs-Differenzialgleichung, die gemeinsam mit den Anfangsbedingungen das folgende nichtlineare Anfangswertproblem definiert:
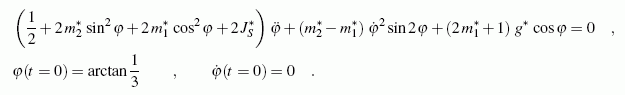
Damit ist der weitere Lösungsweg klar:
- Die (natürlich nur numerisch mögliche) Lösung des Anfangswertproblems liefert das Bewegungsgesetz φ(t) und auch die benötigten Ableitungen nach der Zeit.
- Mit dem bekannten Bewegungsgesetz φ(t) können alle Beschleunigungen mit Hilfe der Zwangsbedingungen berechnet werden.
- Mit den bekannten Beschleunigungen können die Komponenten der Bolzenkräfte nach den oben angegebenen Formeln berechnet werden, aus denen sich schließlich die resultierenden Bolzenkräfte ergeben:
Lösung mit Matlab
Das Anfangswertproblem 2. Ordnung muss für die Lösung mit Matlab in ein System 1. Ordnung umgeschrieben werden. Dafür wird eine neue Variable ω als Ableitung der Winkelkoordinate φ nach der Zeit eingeführt:
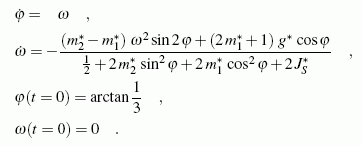
Mit dem folgenden Matlab-Script wird der oben beschriebene Lösungsweg realisiert:
global JSS m1S m2S gS
JSS = 1/12 ; m1S = 0.5 ; m2S = 2 ; gS = 29.43 ;
maxstep = 0.001 ;
phi0 = [asin(1/3) ; 0] ; tspan = [0 2] ; % Anfangswerte, Zeitintervall
options = odeset ('MaxStep' , maxstep) ; % Integration des AWPs:
[t phiphip] = ode45 (@Dgl , tspan , phi0 , options) ;
phi = phiphip(:,1) ; phip = phiphip(:,2) ; % Sortieren der Ergebnisse
zaehl = -((m2S-m1S)*(phip.^2).*sin(2*phi)+(2*m1S+1)*gS*cos(phi)) ;
nenn = (0.5+2*m2S*(sin(phi)).^2+2*m1S*(cos(phi)).^2+2*JSS) ;
phipp = zaehl./nenn ;
xppS = -(phipp.*sin(phi)+(phip.^2).*cos(phi))/2 ;
yppS = (phipp.*cos(phi)-phip.^2.*sin(phi))/2 ;
x2ppS = -(phipp.*sin(phi)+phip.^2.*cos(phi)) ;
y1ppS = (phipp.*cos(phi)-phip.^2.*sin(phi)) ;
F1xS = (xppS+m2S*x2ppS)/gS ;
F1yS = m1S+m1S*y1ppS/gS ;
F2xS = m2S*x2ppS/gS ;
F2yS = 1+yppS/gS+m1S+m1S*y1ppS/gS ;
F1S = sqrt(F1xS.^2+F1yS.^2) ;
F2S = sqrt(F2xS.^2+F2yS.^2) ;
subplot(2,2,1) ; plot (t , phi) , grid on , title ('\phi(t)')
subplot(2,2,3) ; plot (t , phip) , grid on , title ('\omega(t)')
subplot(2,2,2) ; plot (t , F1S) , grid on , title ('F_1^{\ast}(t)')
subplot(2,2,4) ; plot (t , F2S) , grid on , title ('F_2^{\ast}(t)')
disp([' ']) ;
disp(['Rechnung mit MaxStep = ' , num2str(maxstep) , ':']) ;
disp(['phi (t_end = ' , num2str(t(end)) , ') = ' , num2str(phi(end))]) ;
disp(['omega(t_end = ' , num2str(t(end)) , ') = ' , num2str(phip(end))]) ;
% ============================================================
% Function, die die "rechte Seite" des Dgl.-Systems definiert:
function f = Dgl (t , phiphip)
global JSS m1S m2S gS
phi = phiphip(1) ;
omega = phiphip(2) ;
phiP = omega ;
zaehl = -((m2S-m1S)*omega^2*sin(2*phi)+(2*m1S+1)*gS*cos(phi)) ;
nenn = (0.5+2*m2S*(sin(phi))^2+2*m1S*(cos(phi))^2+2*JSS) ;
f = [phiP ; zaehl/nenn] ;
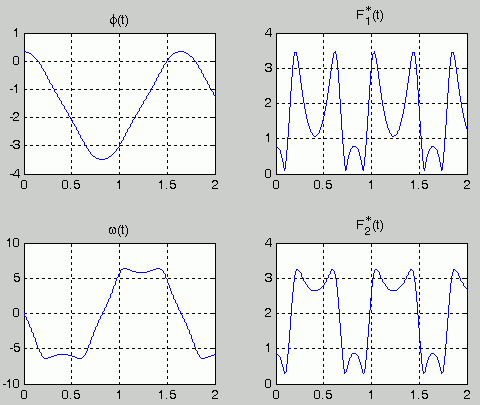
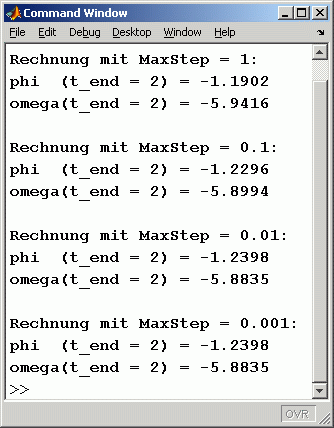
Zu diesem Script: Das Setzen der MaxStep-Option ist (wie bei fast allen Anfangswertproblemen der Technischen Mechanik) zwingend, weil die Standardeinstellung keine ausreichende Genauigkeit bringt. Welcher Wert dafür einzusetzen ist, wird durch Mehrfachrechnung ausprobiert. Dafür werden die Endwerte für φ und ω in das Command Window ausgegeben und für die unterschiedlichen Rechnungen verglichen. Nachfolgend sieht man links die Graphik-Ausgabe des Scripts und rechts die Werte im Command Window für insgesamt vier Rechnungen. Man erkennt, dass die Standardeinstellung (MaxSteP = 1) nicht ausreichend ist, mit MaxSteP = 0,01 erhält man Ergebnisse, die sich bei noch kleineren Werten nicht mehr ändern:
|
|
Ergebnis verifizieren
Die oben beschriebene Mehrfachrechnung mit unterschiedlich feinen Schrittweiten liefert nur ein Indiz dafür, dass die numerische Rechnung "gesund" ist. Weil es aber bei Problemen dieser Art außerordentlich viele Fehlerquellen gibt, wird im Kapitel "Kinetik starrer Körper" empfohlen, eine Kontrolle mit Hilfe des Energiesatzes einzubauen.
Die nebenstehende Skizze zeigt zwei Lagen des Systems, für die die Energiebilanz besonders einfach zu formulieren ist. Als Zustand 1 wird der Start der Bewegung und als Zustand 2 die horizontale Lage der Stange betrachtet. Die Energiebilanz liefert unmittelbar eine Beziehung zwischen Weg und Geschwindigkeit, hier zum Beispiel die Winkelgeschwindigkeit der Verbindungsstange beim Passieren der Lage φ = 0. Damit können die durch numerische Integration gewonnenen Werte punktuell kontrolliert werden.
Allerdings liefert die numerische Integration des Anfangswertproblems das Bewegungsgesetz in Abhängigkeit von der Zeit, so dass die Nullstelle von φ(t) benötigt wird. Für diese Aufgabe bietet Matlab mit der Event-Strategie eine effektive Möglichkeit Lösungsmöglichkeit. Dies wird für die hier behandelte Aufgabe auf einer eigenen Seite demonstriert.
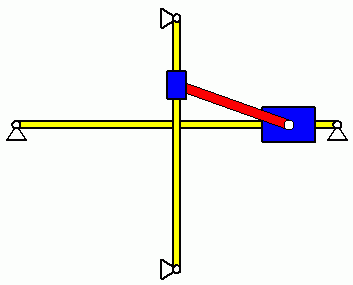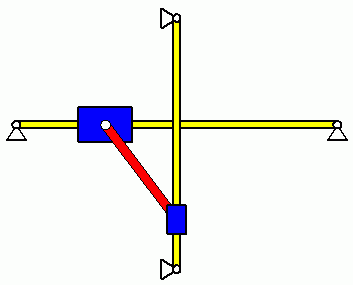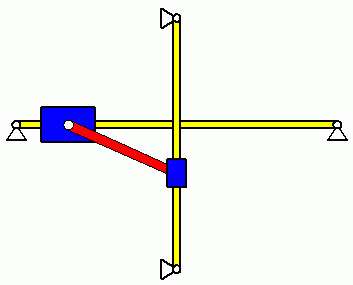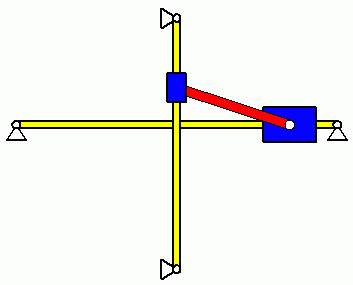
Die oben zu sehenden Diagramme φ(t) und ω(t) sind schwierig zu interpretieren. Immerhin zeigt sich bereits der zu erwartende periodische Verlauf und die Erfüllung der Anfangsbedingungen. Eine Vorstellung vom zu erwartenden Bewegungsverlauf hätte man allerdings eher für die beiden Gleitsteine.
Die nebenstehende Animation zeigt die Bewegung des Systems. Zumindest die Frage, ob der Bewegungsablauf sinnvoll und in dieser Form vorstellbar ist, kann mit einer solchen Animation, erzeugt mit den berechneten Daten, besonders einfach beantwortet werden. Und wenn man sich über die kurzen Hin- und Herbewegungen des Gleitsteins auf der horizontalen Führung jeweils in der Nähe seiner Extremlagen wundert: Neben der oben angekündigten Kontrolle der Winkelgeschwindigkeit werden auf der Seite Verifizieren der Lösung eines Anfangswertproblems auch die Bewegungsgesetze der Gleitsteine analysiert.
