|
|
||||||||||||||||||||||||
|
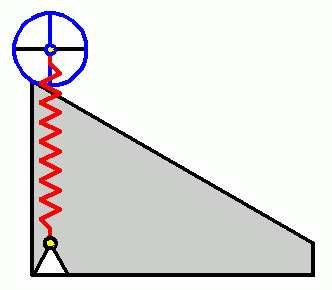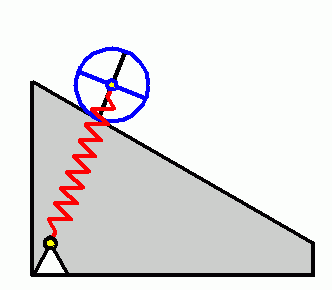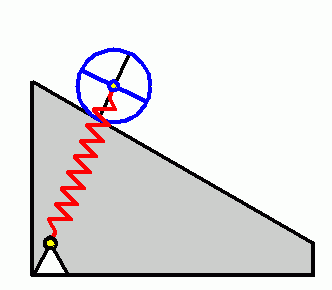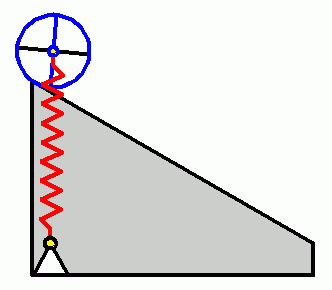
Nach Durchtrennen des Haltefadens beginnt die Walze eine reine Rollbewegung auf der schiefen Ebene. Geg.: c = 12 N/mm , b = 80 cm , α = 30° . Die Bewegung der Walze wird mit einer Koordinate x beschrieben, die die Lage des Mittelpunktes der Walze verfolgt, parallel zur schiefen Ebene gerichtet ist und ihren Ursprung in der skizzierten Ruhelage des Systems hat. Während der Bewegung der Walze verändert die von der Feder auf die Walze ausgeübte Kraft ständig ihre Richtung und ihre Größe. Die rechte Skizze zeigt die geometrischen Verhältnisse. In dem Dreieck sind b die Länge der entspannten Feder, x die Bewegungskoordinate und lc die aktuelle Länge der Feder. Diese kann z. B. mit dem Kosinussatz berechnet werden:
Auf dem gleichen Weg kann man den Winkel β, der die Richtung der Federkraft bezüglich der Richtung der schiefen Ebene festlegt, berechnen:
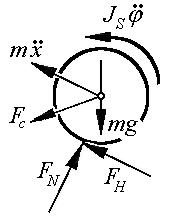
Nach diesen Vorüberlegungen kann mit einem geeigneten Verfahren (z. B.: Prinzip von d’Alembert, vgl. z. B.: "Dankert/Dankert: Technische Mechanik", Seite 541) die Bewegungsdifferenzialgleichung aufgeschrieben werden. Die nebenstehende Skizze zeigt die nach dem Prinzip von d’Alembert anzutragenden Kräfte und Momente. Als Gleichgewichtsbedingung wird das Momentengleichgewicht um den Momentanpol formuliert (Angriffspunkt von Normalkraft und Haftkraft, um diese beiden nicht interessierenden Größen aus der Rechnung herauszuhalten):
Mit der Rollbedingung und der Formel für das Massenträgheitsmoment der zylindrischen Walze
lässt sich die Gleichgewichtsbedingung umformen zur Bewegungsdifferenzialgleichung
wobei zu beachten ist, dass die Koordinate x auch noch in Fc und β steckt. Es sind die Bewegungsgesetze x(t) und v(t) für ein Zeitintervall t = 0 ... 10 s zu ermitteln und graphisch darzustellen. Die Bewegungsdiferenzialgleichung ist sowohl mit einem numerischen Integrationsverfahren mit konstanter Schrittweite (z. B. Runge-Kutta-Verfahren 4. Ordnung) zu integrieren als auch mit einem Verfahren mit variabler Schrittweite (z. B. mit der Matlab-ode45-Function). In beiden Fällen ist zu ermitteln, welche Schrittweite (bzw. welche Einstellung für die Schrittweitensteuerung) erforderlich ist, um ausreichend genaue Ergebnisse auch noch am Ende des Integrationsintervalls zu erhalten.
x1 = 0,1292179216 m ; x2 = 0,2334628275159 m ; x3 = 0,8687086977 m . Man bestätige diese Ergebnisse durch folgendes "numerisches Experiment": Die Rechnung mit dem Matlab -Script ist mit diesen Werten als Anfangsauslenkung der Masse m zu starten. Die sich einstellenden "Bewegungen" sind zu interpretieren. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

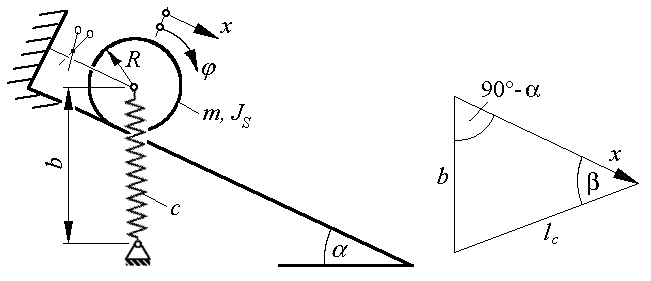 Eine zylindrische Walze (Masse m, Massenträgheitsmoment bezüglich des Schwerpunkts JS) ist durch eine lineare Feder
gefesselt und wird auf einer schiefen Ebene durch einen Haltefaden in Ruhe gehalten. In dieser Lage ist die Feder der Länge b entspannt.
Eine zylindrische Walze (Masse m, Massenträgheitsmoment bezüglich des Schwerpunkts JS) ist durch eine lineare Feder
gefesselt und wird auf einer schiefen Ebene durch einen Haltefaden in Ruhe gehalten. In dieser Lage ist die Feder der Länge b entspannt.
 Die Federkraft erhält man aus dem Produkt der Federsteifigkeit c und der Differenz aus aktueller Federlänge lc und der Länge
der entspannten Feder b:
Die Federkraft erhält man aus dem Produkt der Federsteifigkeit c und der Differenz aus aktueller Federlänge lc und der Länge
der entspannten Feder b:
 Die o. g. Berechnungen sind sowohl für eine Walze mit der Masse m = 40 kg als auch für eine Walze mit
der Masse m = 50 kg auszuführen. Die unterschiedlichen Bewegungsgesetze sind zu interpretieren.
Die o. g. Berechnungen sind sowohl für eine Walze mit der Masse m = 40 kg als auch für eine Walze mit
der Masse m = 50 kg auszuführen. Die unterschiedlichen Bewegungsgesetze sind zu interpretieren.


