|
|
||||||||||||||||||||||||
|
wird durch Einführen einer neuen Variablen für die Geschwindigkeit zu einem Differenzialgleichungssystem 1. Ordnung:
Die für die Aufgabenstellung c benötigte Beziehung für die Gesamtenergie des Systems wird unter der Annahme formuliert, dass das Null-Potenzial (willkürlich) in Höhe des Mittelpunktes der Walze in der Ausgangslage festgesetzt wird:
Das nachfolgende Matlab-Script realisiert die Berechnung sowohl mit dem Runge-Kutta-Verfahren 4. Ordnung als auch mit der Matlab-ode45-Function. |
|
|
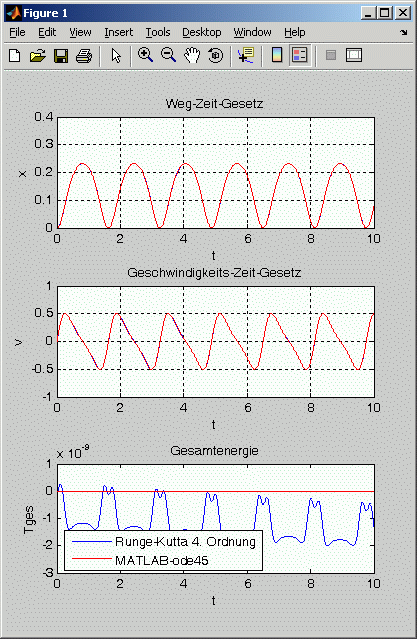
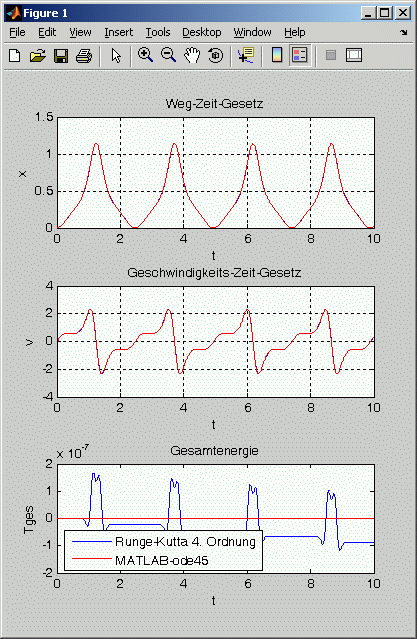
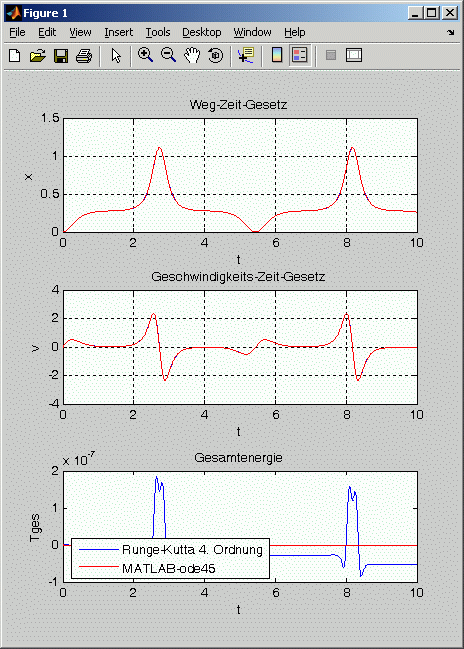
Aufgabenstellung a: Die graphischen Darstellung der Bewegungsgesetze für die Bewegung der Masse m = 40 kg ist nachfolgend links zu sehen, für die Bewegung der Masse m = 50 kg rechts:
Für m = 40 kg ergibt sich nur eine Schwingung mit kleinem Ausschlag, eine Masse m = 50 kg dagegen kann sich an der Stelle, an der die Feder besonders stark zusammengedrückt wird, "vorbeidrängeln" und führt eine Schwingung mit recht großer Maximalauslenkung aus. Wenn die Auslenkung x und die Geschwindigkeit v am Ende des Zeitintervalls mit drei Stellen Genauigkeit als Kriterien für ausreichend feine Diskretisierung verwendet werden, hat man für m = 40 kg ab 400 Runge-Kutta-Schritten bzw. mit maxstep=0,05 stabile Ergebnisse, für m = 50 kg erst ab 2000 Runge-Kutta-Schritten bzw. mit maxstep=0,01.
Aufgabenstellung b: Eine Masse m = 41 kg schafft es gerade so mit großer Mühe, sich an der kritischen Stelle "vorbeizudrängeln" (eine Masse m = 40,99 kg schafft es schon nicht mehr), wobei die Geschwindigkeit jeweils für etwa 1 s annähernd Null ist (nebenstehende Graphik). Dies ist numerisch sehr kritisch, deshalb werden für stabile Ergebnisse wesentlich mehr Integrationsschritte benötigt als für m = 40 kg. Ab 3000 Runge-Kutta-Schritten bzw. ab maxstep=0,005 sind aber auch für diesen Fall die Ergebnisse stabil.
Aufgabenstellung c: Die graphische Ausgabe der oben angegebenen Funktion für die Gesamtenergie, die im gesamten Bereich konstant bei Null liegen müsste (weil das Null-Potenzial auf die Höhe der Ausgangslage gelegt wurde und dort auch die kinetische Energie Null ist), zeigt nur sehr kleine Abweichungen. Allerdings sieht man sehr deutlich, dass die Abweichungen in den Bereichen großer Koordinaten- und Geschwindigkeitsänderungen liegen. Mit Skepsis muss man jedoch für eine Rechnung über ein größeres Zeitintervall einen Verlauf betrachten, wie er nebenstehend für die Runge-Kutta-Rechnung zu sehen ist: Wenn nach jedem "Störungsbereich" die Gesamtenergie kleiner wird, dann kann das nicht sehr lange gut gehen.
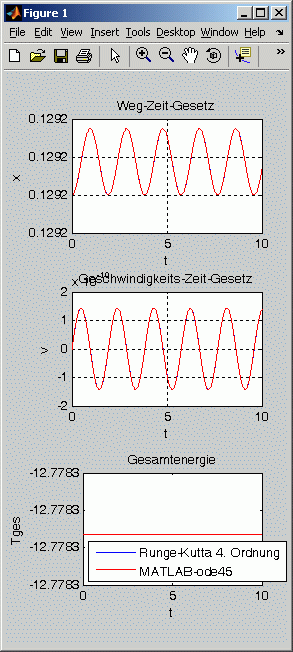
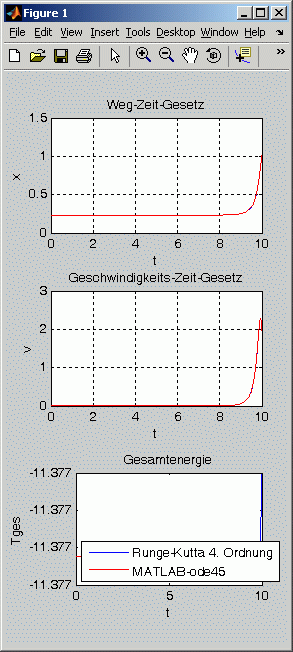
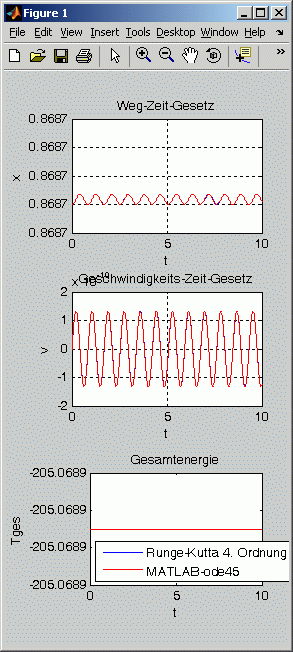
Aufgabenstellung d: Die Rechnungen mit den Anfangsbedingungen x1 bzw. x3 zeigen Schwingungen mit extrem kleinen Ausschlägen (nachfolgende Graphiken links und rechts). Dies liegt daran, dass trotz der vielen angegebenen Stellen die Werte doch noch geringfügig gerundet sind, so dass ganz kleine Abweichungen von der statischen Gleichgewichtslage zu den Bewegungen führen. Es wird aber dadurch auch bestätigt, dass diese statischen Gleichgewichtslagen stabil sind: Bei stabilem Gleichgewicht führen kleine Störungen zu einer Rückkehr in die Gleichgewichtslage. Anders ist die Situation bei der Anfangsbedingung x2 (nachfolgend die mittlere Graphik): Hier bleibt die Masse etwa 8 s scheinbar in Ruhe, um danach die Gleichgewichtslage zu verlassen. Diese Gleichgewichtslage ist instabil.
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

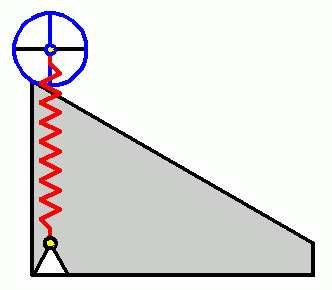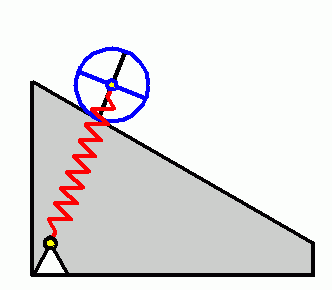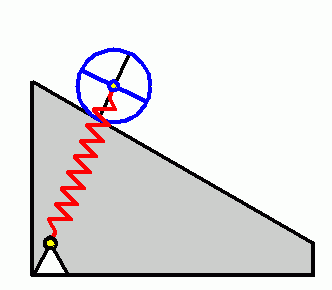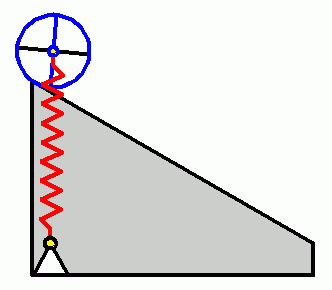
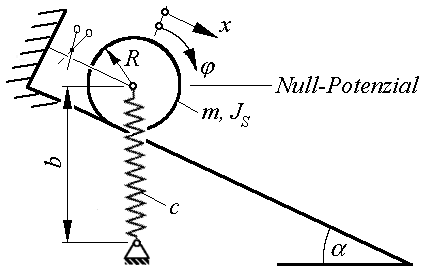 Die Bewegungsdifferenzialgleichung
Die Bewegungsdifferenzialgleichung
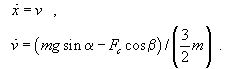
 Das oben gelistete MATLAB-Script steht als
Das oben gelistete MATLAB-Script steht als



