
Aufgabe
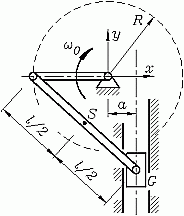
Der skizzierte Mechanismus (exzentrische Schubkurbel) ist ein System aus drei starren Körpern. Die Kurbel dreht sich mit der konstanten Winkelgeschwindigkeit ω0 und befindet sich zum Zeitpunkt t = 0 in der dargestellten Lage.
Gegeben: R , l , a , ω0 .
Für den Gleitstein G und den Mittelpunkt S der Verbindungsstange sollen die Geschwindigkeits-Zeit-Gesetze vG(t) bzw. vS(t), für die Verbindungsstange auch das Winkelgeschwindigkeits-Zeit-Gesetz ωS(t) ermittelt werden.
Bewegungsgesetze
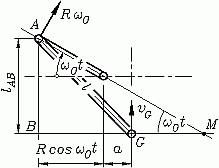
Die nebenstehende Skizze zeigt das System zum Zeitpunkt t, die Kurbel hat sich um den Winkel ω0t gedreht. Für die Verbindungsstange sind zwei Geschwindigkeitsrichtungen bekannt: Ihr Momentanpol M ist der Schnittpunkt der Senkrechten zur Bewegungsrichtung des Punktes G und der Senkrechten zur Bewegungsrichtung des Punktes A, der auf dem Kurbelkreis mit der konstanten Bahngeschwindigkeit Rω0 umläuft (Geschwindigkeit ist tangential zum Kreis mit dem Radius R gerichtet).
Auf der Basis dieser Skizze werden im Kapitel "Kinematik starrer Körper" die Winkelgeschwindigkeit der Verbindungsstange ωS und die Geschwindigkeit des Gleitsteins vG berechnet Für die gesamte Rechnung wird nachdrücklich empfohlen, nicht den Ehrgeiz zu haben, durch "Aufschreiben, Einsetzen und Vereinfachen" zu möglichst "schönen Endformeln" zu kommen, weil sich das bei den recht unhandlichen Beziehungen, wie sie für solche kinematischen Verhältnisse typisch sind, häufig durch Rechenfehler rächt. Man sollte man mit einem "Funktionensatz" arbeiten, der sich dadurch auszeichnet, dass alle Funktionen (neben der unabhängigen Variablen, hier ist das die Zeit t) nur die gegebenen Größen und die vorab definierten Funktionen enthalten. Außerdem sollte man die Operationen, für die das möglich ist, dem Computer übertragen (zum Beispiel das Bilden von Ableitungen). Hier werden nur die Ergebnisse angegeben:
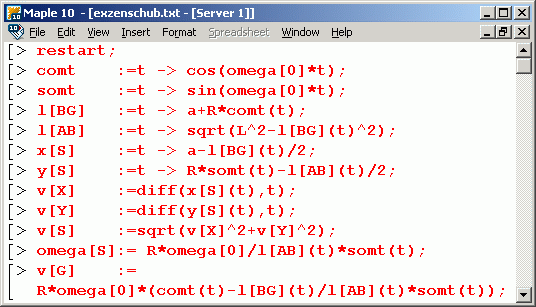
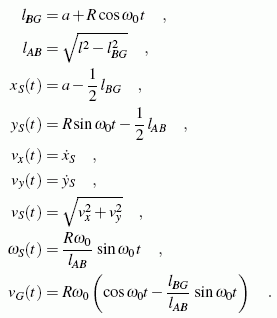
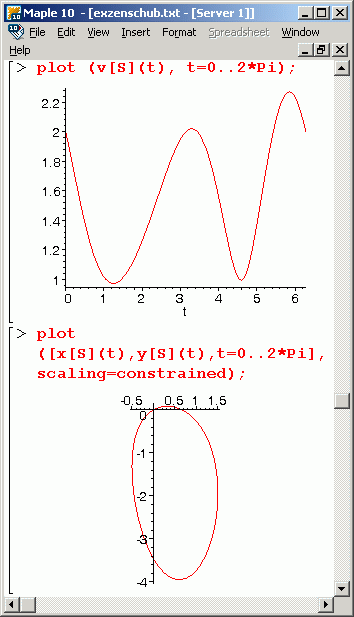
Neben den Formeln ist das Maple-Script für diesen Formelsatz zu sehen (zum Download verfügbar als exzenschub.mws). Weil Maple symbolisch rechnet, kann er ausgewertet werden, ohne Zahlenwerte für die gegebenen Größen vorzugeben. Nachstehend wird die Ausgabe nach Abarbeitung der drei letzten Zeilen gezeigt:
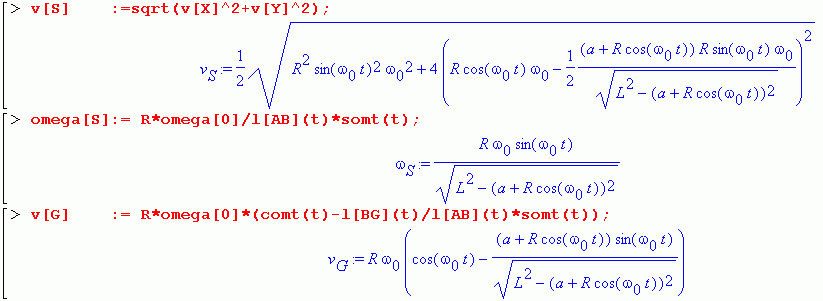
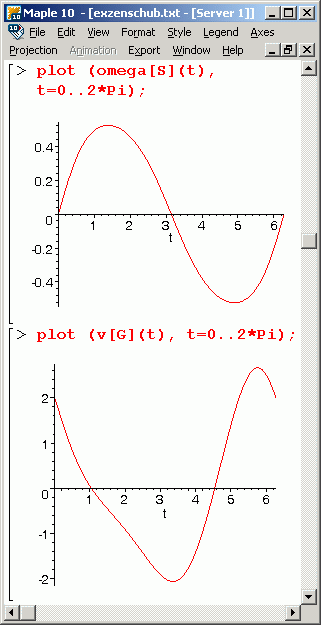
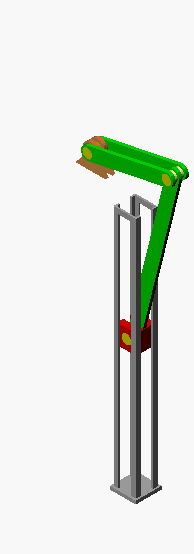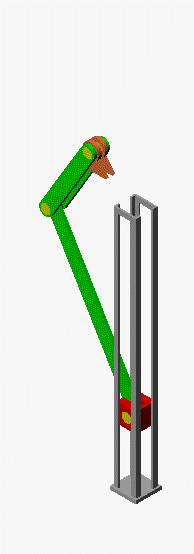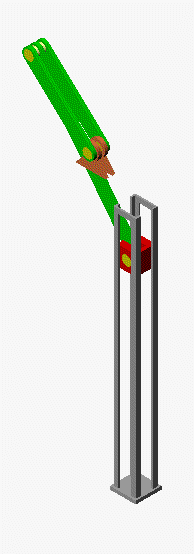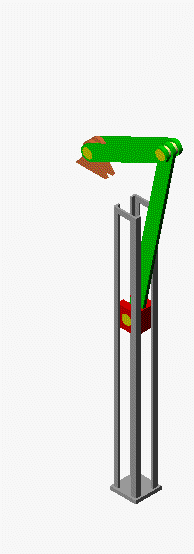
Für die graphische Darstellung der Funktionen werden Zahlenwerte für die gegebenen Größen benötigt. Wie im Kapitel "Kinematik starrer Körper" werden die Abmessungsverhältnisse R/a = 2 und l/a = 4 angenommen, um die nachfolgenden Graphiken zu erstellen. Links sieht man die Funktionen ωS(t) und vG(t), rechts vS(t) und die Bahnkurve des Mittelpunkts der Verbindungsstange. Zwischen den beiden Bildern mit den Maple-Graphiken sieht man eine Animation der Bewegung.
|
|
|
