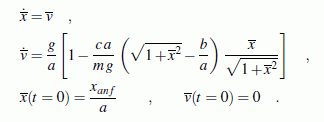
Aufgabe

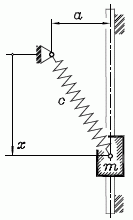
Ein Gleitstein mit der Masse m kann auf einer vertikalen Führung reibungsfrei gleiten. Er ist durch eine (lineare) Feder gefesselt, die im entspannten Zustand die Länge b hat. Der Gleitstein wird um x_anf ausgelenkt und zum Zeitpunkt t = 0 ohne Anfangsgeschwindigkeit freigelassen.

Für das Intervall 0 ≤ t ≤ 20s sollen die Bewegungsgesetze x(t) für die Anfangsauslenkungen

ermittelt werden.

Anfangswertproblem

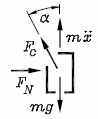
Die Skizze zeigt die freigeschnittene Masse mit den an ihr wirkenden Kräften. Die Gleichgewichtsbedingung in vertikaler Richtung liefert:

Nach Einführen einer dimensionslosen Bewegungskoordinate x = x/a kann das folgende Anfangswertproblem formuliert werden:

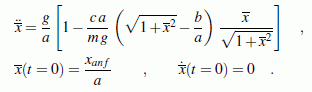
Weil die nachfolgend genutzten Software-Produkte nur Anfangswertprobleme 1. Ordnung verarbeiten können, wird durch Einführen einer Geschwindigkeit v als Ableitung von x nach der Zeit ein Anfangswertproblem, das in dieser Form den Programmen angeboten werden kann:

Lösung des Anfangswertproblems

Student Eugen Lass (HAW Hamburg, Betreuer: Prof. Dr. Thomas Frischgesell) hat die Aufgabe mit Matlab gelöst