Eine Viergelenkkette wird definiert durch die Lage der beiden Lager A und D (Angabe der Koordinaten x_A und y_A des Punktes A in einem Koordinatensystem mit dem Ursprung in D) und die Längen der drei Glieder a, b und c.

Die Viergelenkkette wird durch das Glied AB angetrieben, diese Kurbel rotiert mit konstanter Winkelgeschwindigkeit, die aktuelle Stellung wird durch den Winkel φ beschrieben. Mit der Koppel BC ist der "Koppelpunkt K" starr verbunden. Seine Lage wird durch die Abmessungen b₁ und b₂ bestimmt, die von ihm beschriebene Bahn wird während der Bewegung gezeichnet. Die Abmessungen, die über die Eingabefelder geändert werden können, entnimmt man der folgenden Sizze:

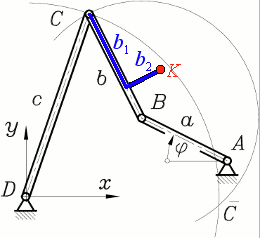
Die Werte für a, b und c müssen größer als Null sein, b₁ und b₂ dürfen beliebige (positive oder negative Werte) annehmen.

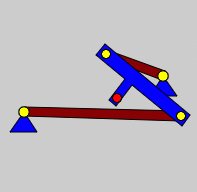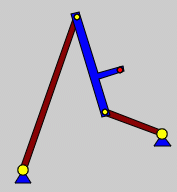
Kurbelschwinge, wie sie beim Start des Programms erscheint (links) und die alternative Startstellung

Es gibt zwei unterschiedliche Startstellungen

Nicht jede Abmessungskombination ist realisierbar. Nach Eingabe der Abmessungen und des Winkels φ (Anfangsstellung der Kurbel AB) wird überprüft, ob diese Viergelenkkette mit dieser Kurbelstellung überhaupt möglich ist. Wenn der Test positiv ausfällt, wird die Viergelenkkette gezeichnet.

In der Regel sind zu jeder Stellung φ zwei verschiedene Lagen der drei Glieder möglich. Man erreicht die jeweils andere Lage, wenn man auf den Button "Alternative Startstellung" klickt. Die beiden Startstellungen führen zu unterschiedlichen Bewegungsabläufen.

Spezialfälle der Viergelenkketten

Nachfolgend werden einige Spezialfälle der Viergelenkketten vorgestellt. Durch Klicken auf das jeweilige Bild werden die Abmessungen für einen entsprechenden Spezialfall in das Animationsbild übertragen, und die Animation kann gestartet werden.

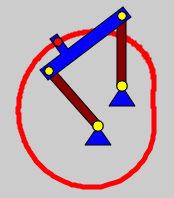
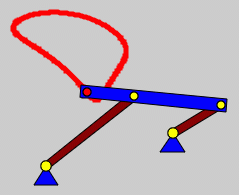
Bei einer Doppelkurbel können sowohl die Antriebskurbel als auch das andere gelagerte Getriebeglied komplett umlaufen.			Bei einer Kurbelschwinge kann nur die Antriebskurbel komplett umlaufen, während das andere gelagerte Getriebeglied nur in einem gewissen Winkelbereich hin und her schwingt.
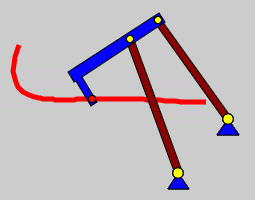
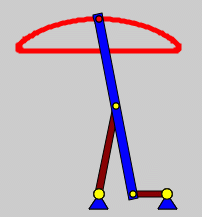
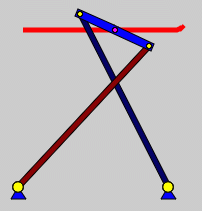
Bei einer Doppelschwinge können beide gelagerten Getriebeglieder nur in einem begrenzten Winkelbereich hin- und herschwingen. Mit den hier gezeigten Abmessungen bewegt sich der Koppelpunkt in einem gewissen Bereich auf einer horizontalen Geraden (Wippkran-Mechanismus).			Der Tschebyscheff-Lambda-Mechanismus erzeugt eine Koppelkurve, die sich vorzüglich für den Antrieb von "Laufmaschinen" eignet: Ein Bereich wird auf einer fast idealen horizontalen Geraden mit annähernd konstanter Geschwindigkeit durchlaufen (Fuß befindet sich am Boden), die entgegengesetzte Bewegung wird deutlich schneller absolviert.
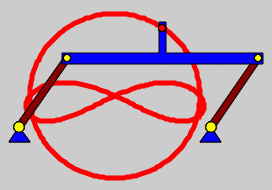
Die Parallelkurbel ist ein Sonderfall der Doppelkurbel mit der Besonderheit, dass es Stellungen gibt, in denen unterschiedliche Fortsetzungen der Bewegung möglich sind. Bei der skizzierten Parallelkurbel sind in den Stellungen φ=0° und φ=180° der Antriebskurbel solche Verzweigungen möglich. Es erscheint am unteren Rand des Eingabebereichs das Angebot, die Verzweigungsmöglichkeit zu nutzen.			Mit dem Tschebyscheff-Kreuzlenker kann sich der Mittelpunkt der Koppel auf einer annähernd geraden Linie bewegen.
Hinweis: Die Animation einer Viergelenkkette kann nur numerisch realisiert werden, zum Beispiel muss die kontinuierliche Antriebsbewegung mit endlichen Schritten programmiert werden (Einstellung beim Start des Programm ist eine Schrittweite von 1°). Die Berechnung der Lage der Getriebeglieder für eine bestimmte Stellung der Antriebskurbel ist recht aufwändig. Auf der Seite "Viergelenkketten" wird auf dieses Problem hingewiesen. Daraus resultiert, dass alle Abfragen im Animationsprogramm nur mit Näherungswerten ausgeführt werden können. Ganz speziell bei Viergelenkketten wie Parallelkurbeln kann es vorkommen, dass die Verzweigungspunkte nicht genau getroffen und/oder nicht erkannt werden. Aber auch dann, wenn es passiert, dass die Fortsetzung der Bewegung überraschend erscheint, ist es immer eine mögliche Bewegung.

Eine interessante geometrische Besonderheit

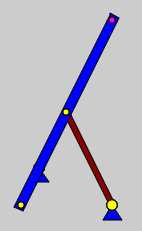
Karl Hovekamp machte auf die in der Skizze links zu sehende Besonderheit aufmerksam (Skizze wurde seiner Seite http://www.hovekamp.info/ entnommen): In einem beliebigen Quadrat entsteht durch die Verbindung zweier Ecken mit den gegenüberliegenden Seitenmitten ein rechtwinkliges Dreieck.

Die eigentlich überraschende Besonderheit besteht aber darin, dass in dieser Figur der Tschebyscheff-Lambda-Mechanismus steckt. Der Bildschirm-Schnappschuss (rechts) verdeutlicht dies: Das Lager A mit der Kurbel AB befindet sich am Punkt, wo der rechte Winkel des Dreiecks liegt (B ist der Punkt unten links). Lager und Kurbel sind teilweise bzw. völlig von der (blauen) Koppel verdeckt. Das Lager D mit der Schwinge DC liegt im Punkt rechts unten. Der Koppelpunkt K gehört nicht zu dem links zu sehenden Quadrat, liegt auf der Verlängerung der Koppel BC.

Klick auf den nachfolgenden Button transportiert die Abmessungen dieses Tschebyscheff-Lambda-Mechanismus in die Eingabefelder des Animationsfeldes oben.