Stabilität von Gleichgewichtslagen

Aufgabe, die in den Kapiteln "Elastische Lager" und "Prinzipien der Mechanik" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" behandelt wird:

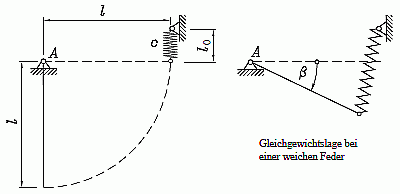
Ein starrer Stab (Länge l, Gewichtskraft mg greift im Mittelpunkt des Stabes an) ist bei A drehbar gelagert. Er wird in eine Feder (Federkonstante c) eingehängt, deren Länge l₀ (unbelastet) sich dadurch erheblich vergrößert. Man ermittle die möglichen Gleichgewichtslagen, die wie skizziert durch den Winkel β beschrieben werden sollen.

Animation starten durch Klick auf den folgenden Button:

Für die Parameter, die beim Start der Seite gelten, existieren 4 Gleichgewichtslagen. Nach Klick auf den blau/roten Punkt am Ende des Stabes (färbt sich dabei rot) kann man den Stab bei gedrückter linker Maustaste bewegen. Dabei bringt man ein zusätzliches Moment auf, mit dem die jeweilige Stellung von Stab und Feder realisiert werden kann.

Weil man über die Maus weder Größe noch Drehsinn des Moments "spürt", werden diese Informationen über das Feld "M =" und einen Pfeil in der Grafik verdeutlicht. Bei jedem Nulldurchgang des Moments existiert ein Gleichgewichtslage. Nach Lösen der linken Maustaste sind zwei unterschiedliche Reaktionen möglich:

Wenn es eine stabile Gleichgewichtslage ist, bleiben Stab und Feder in dieser Lage in Ruhe.
Wenn es eine instabile Gleichgewichtslage ist, schwingt der Stab in eine stabile Gleichgewichtslage.

Winkel β = ° für die dargestellte Lage
kann nur durch ein Moment M = Nm gehalten werden.

Die aktuellen Systemparameter sieht man in den folgenden Eingabefeldern. Sie können modifiziert werden.

Länge des Stabes:	l =	m
Gewichtskraft des Stabes:	mg =	N
Länge der ungedehnten Feder:	l₀ =	m
Federsteifigkeit:	c =	N/m

Hinweis

Das Problem wird in verschiedenen Kapiteln des Lehrbuchs "Dankert/Dankert: Technische Mechanik" mit unterschiedlichen theoretischen Zugängen behandelt:

Im Kapitel "Elastische Lager" werden die Gleichgewichtsbedingungen am verformten System formuliert. Der Formelsatz wird auf der Seite "Gleichgewicht bei einer weichen Feder" ausgewertet.
Im Kapitel "Prinzipien der Mechanik" wird gezeigt, dass Gleichgewicht nur möglich ist, wenn die im System gespeicherte potenzielle Energie einen Extremwert annimmt. Aus der Art des Extremums (Minimum oder Maximum) kann auf die Stabilität geschlossen werden. Die Energiefunktion wird auf der Seite "Stabilität von Gleichgewichtslagen" ausgewertet.

Auf den beiden genannten Seiten wird jeweils der Fall numerisch ausgewertet, der hier nach dem Start der Seite oben rechts dargestellt ist. Dabei ergeben sich vier mögliche Gleichgewichtslagen, von denen zwei stabil und zwei instabil sind:

Vier Gleichgewichtslagen

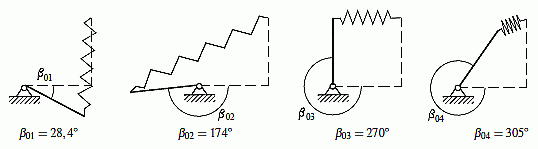
Mit der oben angebotenen interaktiven Animation können die Gleichgewichtslagen bestätigt werden. Wenn man den Stab mit der Maus dreht, sieht man, dass das Moment, das für eine Stellung erforderlich ist, um sie zu halten, bei genau diesen vier Winkeln einen Nulldurchgang hat. Wenn man die linke Maustaste in der Nähe der Stellungen β₀₁ oder β₀₃ löst, pendelt sich der Stab bei genau diesen Werten ein (stabile Gleichgewichtslagen). Im Gegensatz dazu sind β₀₂ oder β₀₄ instabile Gleichgewichtslagen, auch der Versuch, die Maustaste genau an diesen Punkten zu lösen, führt dazu, dass der Stab zu einer der beiden stabilen Gleichgewichtslagen ausweicht.

Durch Änderung der Problemparameter kann man modifizierte Systeme erzeugen. Manche haben nur zwei, andere haben wie das Problem beim Seitenstart vier Gleichgewichtslagen, immer je zur Hälfte stabile bzw. instabile.