Bild vor oder zurück

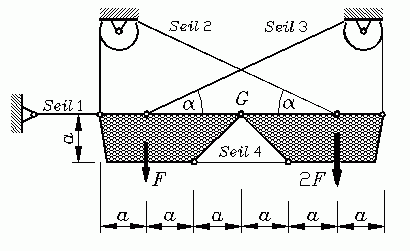
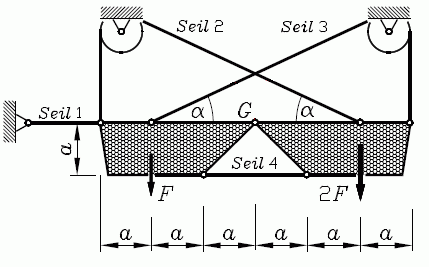
Aufgabe

Zwei starre Körper sind über ein Gelenk G und das Seil 4 miteinander verbunden. Sie sind durch die Kräfte F bzw. 2F belastet und werden von den Seilen 1 bis 3 gehalten. Zu berechnen sind die Seilkräfte.

Gegeben:  F, α = 30°.

Es sind zwei sinnvolle Strategien der Anwendung des Schnittprinzips möglich, die als Varianten a) bzw. b) demonstriert werden.

Variante a)

• Das Starrkörpersystem wird "als Ganzes" durch einen Rundumschnitt, der das Seil 1 einmal und die Seile 2 und 3 je zweimal schneidet, von allen äußeren Bindungen gelöst. Klicken auf den gelben "⇒"-Button zeigt diesen Schnitt.
• Das Gesamtsystem zerfällt durch den Schnitt 1 in vier Teilsysteme (Klicken auf den "⇒"-Button zeigt diese als Systeme I bis IV).
• An jedem Schnittufer werden die Schnittkräfte angetragen, jeweils gleich groß, aber entgegengesetzt gerichtet. Die Systeme I bis III sind noch mit der "Außenwelt" verbunden und werden nicht weiter betrachtet. An den Systemen II und III wird jedoch deutlich, dass die Kräfte in den Seilen von den Rollen nur umgelenkt werden (siehe hierzu auch "Das Problem mit der Rolle"), deshalb tauchen auch am System IV die beiden Seilkräfte F_S2 bzw. F_S3 jeweils doppelt auf.
• Betrachtet wird nun nur noch das von äußeren Bindungen komplett befreite System IV (Klicken auf den "⇒"-Button). An ihm wirken 3 unbekannte Kräfte, die aus drei Gleichgewichtsbedingungen berechnet werden können. Hier werden zwei Kraftgleichgewichts-Bedingungen und das Momentengleichgewicht um den Angriffspunkt des Seils 3 aufgeschrieben. Aus

  

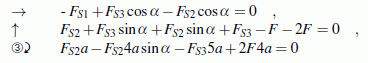
  berechnet man unter Verwendung des gegebenen Werts für den Winkel α die Kräfte in den Seilen 1 bis 3:

  

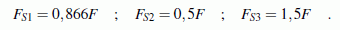
• Für die Berechnung der Seilkraft F_S4 muss ein weiterer Schnitt gelegt werden (ohne Schnitt ist eine Seilkraft nicht sichtbar). Es wird ein Schnitt 2 gelegt, der das Seil 4 und das Gelenk durchtrennt (Klicken auf den "⇒"-Button).
• Durch den Schnitt 2 zerfällt das System IV in die beiden Teilsysteme V und VI (Klicken auf den "⇒"-Button). An den Schnittstellen werden die Seilkraft F_S4 und die Komponenten der Gelenkkraft F_GV und F_GH angetragen (jeweils an den beiden Schnittufern in gleicher Größe, aber entgegengesetzt gerichtet). Beide Systeme sind für beliebige Gleichgewichtsbedingungen zugelassen. Weil nur noch die Seilkraft F_S4 berechnet werden muss, wird zum Beispiel am System V das Momentengleichgewicht um den Gelenkpunkt G formuliert:

  

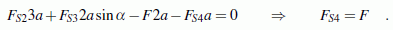
	Bild vor oder zurück

Variante b)

• Alternativ zur oben beschriebenen Variante a) kann man auch gleich das Gesamtsystem in zwei von äußeren Bindungen freie Teilsysteme zerschneiden. Klicken auf den "⇒"-Button zeigt die beiden Schnitte 3 und 4, mit denen das realisiert wird.
• Das System zerfällt in die beiden Teilsysteme V und VI, die den oben bei Variante a) zum Schluss erzeugten Systemen entsprechen (Klicken auf den "⇒"-Button zeigt die beiden Teilsysteme).
• Es gibt nun allerdings einen wesentlichen Unterschied zur Variante a): An keinem der beiden Teilsysteme kann auch nur eine unbekannte Kraft berechnet werden, denn Teilsystem V enthält 6 Unbekannte, beim Teilsystem VI sind es 5 Unbekannte. Es können nur beide Teilsysteme gemeinsam behandelt werden. Für die insgesamt 6 Unbekannten stehen jeweils 3 Gleichgewichtsbedingungen an den Teilsystemen zur Verfügung. Bei 6 Gleichungen mit 6 Unbekannten empfiehlt sich schon die Aufbereitung der Rechnung für den Computer. Dies ist das Gleichungssystem, das von den 6 Gleichgewichtsbedingungen gebildet wird (jeweils Kraftgleichgewicht horizontal und vertikal und Momentengleichgewicht um die Angriffspunkte der schräg angreifenden Seile):

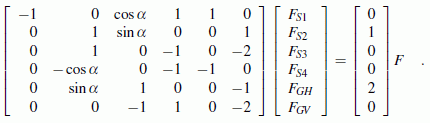
Das Gleichungssystem kann zum Beispiel mit dem Programm "Lineares Gleichungssystem, Matrixinversion" gelöst werden. Nachfolgend sieht man den Bildschirmschnappschuss mit Eingabebereich und Ergebnis:

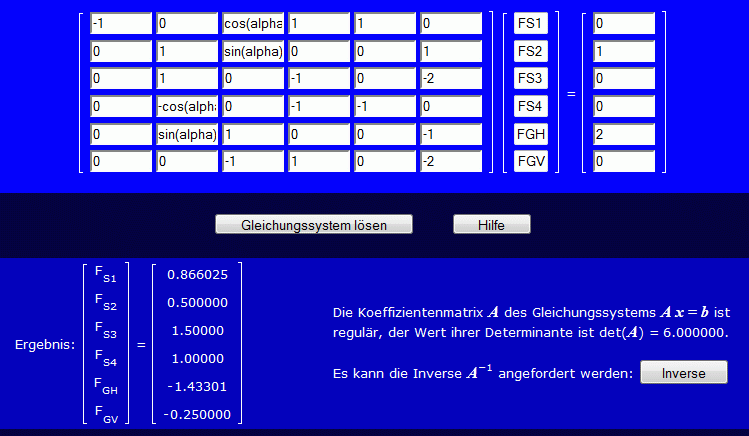
Fazit, Lagerkräfte in den Rollenlagern

Für die Handrechnung ist die Variante a) zu empfehlen: Schnitte so legen, dass man an den entstehenden Teilsystemen die Unbekannten berechnen kann. Variante b) führt häufig auf Gleichungssysteme, deren Lösung "von Hand" zumindest lästig ist. Der Vorteil dieser Variante liegt darin, dass man sich "besonders bequem" aufzuschreibende Gleichgewichtsbedingungen aussuchen kann.

	Bild vor oder zurück

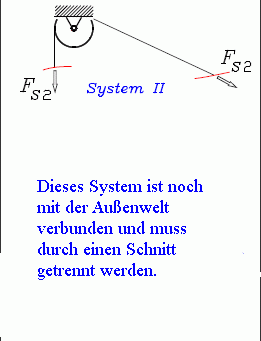
Es soll noch gezeigt werden, wie die Lagerreaktionen der Rollenlager berechnet werden könnten.

• Das nebenstehende Bild zeigt als Beispiel das bereits bei Behandlung der oben demonstrierten Varianten entstandene System II, das noch mit der Außenwelt verbunden ist. Durch einen Schnitt müssen Rolle und Seil vom Lager getrennt werden. Klicken auf den "⇒"-Button zeigt den Schnitt.
• Es entstehen die beiden Teilsysteme VII und VIII. Klicken auf den "⇒"-Button zeigt die beiden Systeme mit den an den Schnittstellen angetragenen Komponenten der Lagerkraft (natürlich wieder an beiden Schnittufern mit der jeweils gleichen Größe, aber entgegengesetzt gerichtet).
• Das System VIII ist frei von äußeren Bindungen, es können die Gleichgewichtsbedingungen formuliert werden. Sinnvoll sind nur die beiden Kraft-Gleichgewichtsbedingungen, denn das Momenten-Gleichgewicht ist automatisch erfüllt, weil an den Seilenden die gleichen Kräfte angetragen wurden. Aus den beiden Gleichgewichtsbedingungen

  

  berechnet man die Komponenten der Lagerkraft: