Aufgabe

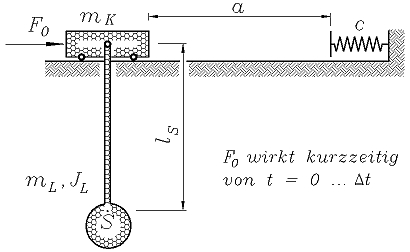
Eine Laufkatze (Masse m_K) trägt eine Last (Masse einschließlich Anhängevorrichtung: m_L, Massenträgheitsmoment bezüglich des Schwerpunktes S: J_L). In der skizzierten Ruhelage beginnt für eine kurze Zeit Δt die konstante Antriebskraft F₀ zu wirken, die danach wieder abgeschaltet wird. Nach dem Zurücklegen der Strecke a stößt die Laufkatze auf einen elastischen Puffer (Federzahl c).

Die Bewegung von Laufkatze und Last soll, beginnend aus der Ruhelage, für die ersten 10 Sekunden analysiert werden.

Gegeben:

m_K = 100 kg ;  J_L = 400 kgm² ;  l_S = 4 m ;  F₀ = 2000 N ;
m_L = 500 kg ;  c = 200000 N/m ;  Δt = 1 s ;  a = 5 m .

Die Aufgabe wird in den Kapiteln "Prinzipien der Mechanik" und "Verifizieren von Computerrechnungen" behandelt.

Bewegungs-Differenzialgleichungen, Vorbereitung der Matlab-Rechnung

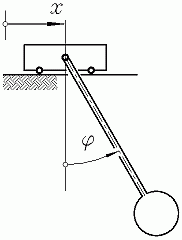
Die Besonderheit dieser Aufgabe besteht in dem Eintreten von "Ereignissen" (Abschalten der Antriebskraft, Zu- und Abschalten einer Feder). Man erfasst sie, indem an die Stelle der Kraft F₀ die zeitabhängige Kraft F_t tritt und die Federkonstante c durch c_t ersetzt wird:

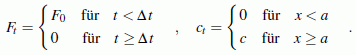
Unter Verwendung der nebenstehend skizzierten Koordinaten gelten folgende Bewegungs-Differenzialgleichungen (die ausführlich kommentierte Herleitung findet man im Kapitel "Prinzipien der Mechanik"):

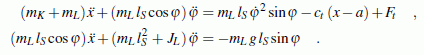
Der verwendete Runge-Kutta-Solver 4. Ordnung für die numerische Integration erwartet ein Differenzialgleichungssystem 1. Ordnung. Deshalb werden die beiden neuen Variablen v und ω eingeführt:

Damit kann das Anfangswertproblem so formuliert werden:

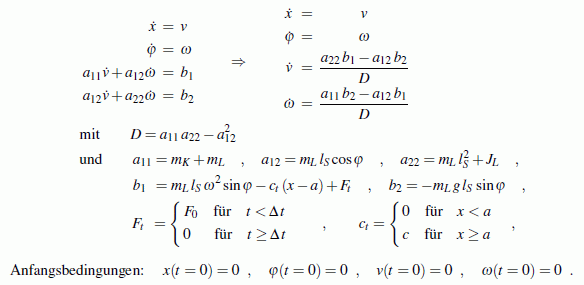
Weil die Differenzialgleichungen für den Runge-Kutta-Solver in Form einer Berechnungsvorschrift für die Ableitungen der gesuchten Funktionen bereitgestellt werden müssen, wurden die beiden in den Beschleunigungsgliedern gekoppelten Gleichungen nach der Cramerschen Regel aufgelöst.

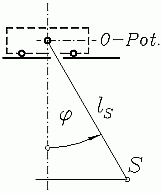
Einer Empfehlung im Kapitel "Verifizieren von Computerrechnungen" folgend, wird eine Energiekurve als Kontrollfunktion zusätzlich berechnet. Die potenzielle Energie soll nur für das bewegte System berücksichtigt werden (während des Kontakts mit der Feder ist auch in dieser potenzielle Energie gespeichert). Im Kapitel "Verifizieren von Computerrechnungen" wird gezeigt, dass mit dem Null-Potenzial entsprechend nebenstehender Skizze und den Anteilen der kinetischen Energie aus der Bewegung von Laufkatze und pendelnder Last folgende Beziehung für die Gesamtenergie des bewegten Systems gilt:

Matlab-Script

Die für die numerische Integration geschriebene Function rk4.m arbeitet mit den klassischen Runge-Kutta-Formeln 4. Ordnung, wie sie im Kapitel "Kinetik des Massenpunktes" für eine Differenzialgleichung angegeben sind, kann aber ein beliebiges Differenzialgleichungssystem mit n Gleichungen 1. Ordnung lösen. Der Function müssen das Integrationsintervall (Anfangs- und Endzeit), ein Vektor mit den Anfangsbedingungen und die Anzahl der Zeitschritte übergeben werden, in die das Integrationsintervall unterteilt werden soll (der Algorithmus arbeitet mit fester Schrittweite). Außerdem muss die Function benannt werden, die die Differenzialgleichungen beschreibt (im folgenden Script: RechteSeite). Abgeliefert werden der Vektor mit den Zeiten, für die Funktionswerte berechnet wurden, und eine Matrix, in der spaltenweise alle berechneten Funktionswerte (hier also x(t), φ(t), v(t) und ω(t)) enthalten sind:

Hinweis: In der Function RechteSeite sind die beiden Zeilen mit den Abfragen, ob die Antriebskraft gerade wirkt und ob gerade Kontakt mit der Feder besteht, farblich hervorgehoben. Diese besonders einfache Realisierung von "Ereignissen" ist hier bei einem Algorithmus, der mit fester Schrittweite arbeitet, unproblemtisch. Diese Aussage steht im Gegensatz zu den Problemen, die bei Algorithmen mit variabler Schrittweite auftreten können. Deshalb wird bei der Verwendung solcher Verfahren (die Matlab-Solver arbeiten so) auf die so genannte "Event"-Strategie verwiesen, die auf der Seite "Laufkatze - Berechnung mit der Event-Strategie" demonstriert wird.

Ergebnisse der Berechnung

Das Matlab-Script gibt die Ergebnisse als graphische Darstellungen und zusätzlich ausgewählte Zahlenwerte in das Command Window aus.

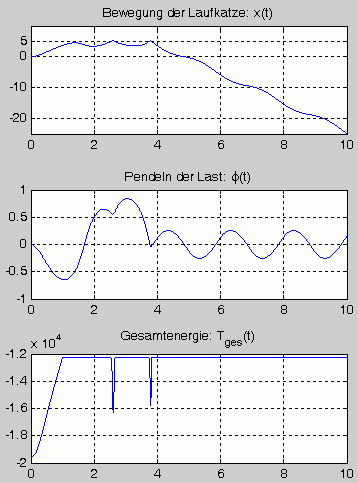
Bei Problemen dieser Art ist auf eine geeignete Schrittweitenwahl zu achten. Hier wurden fünf Rechnungen mit 50, 500, 5000, 50000 und 500000 Schritten durchgeführt. Das ist sicherlich übertrieben, zeigt aber sehr schön, wie sich die Ergebnisse stabilisieren. Die gute Übereinstimmung der Ergebnisse der beiden letzten Rechnungen mit 50000 bzw. 500000 Integrationsschritten zeigt zusätzlich, dass sich die Rundungsfehler bei der gewaltigen Anzahl von Rechenoperationen noch nicht zu einem erkennbaren Fehler kumulieren.

Als Indikatoren können bei jedem beliebigen Anfangswertproblem die berechneten Funktionswerte am Ende des Integrationsintervalls dienen, hier also x(t_end) und φ(t_end). Bei dieser Rechnung kann zusätzlich der Wert für T_ges(t_end) verglichen werden. Diese Indikatoren zeigen, dass mit etwa 5000 Schritten ausreichende Genauigkeit erzielt wird.

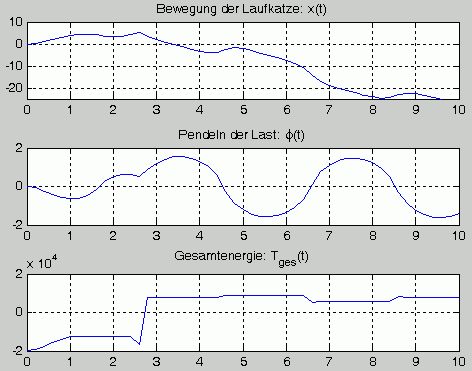
In der Graphik sieht man, dass die Laufkatze offensichtlich zweimal an die Feder stößt, bevor sie ihren Rückweg antritt und mehrmals (auch ohne äußere Krafteinwirkung) ihre Bewegungsrichtung ändert. Dieses etwas überraschende Verhalten wird hier ausführlich diskutiert.

Die Kurve der Kontrollfunktion T_ges(t) liefert ein weiteres Indiz für die Richtigkeit der Rechnung: Startend mit der (negativen) potenziellen Energie, wächst sie infolge der Antriebskraft auf ihren Maximalwert, den sie zum Zeitpunkt t = Δt erreicht. Die beiden "Zacken" in der Kurve kennzeichnen die Energieabgabe an die Feder nach dem Anschlag. Die Energie wird komplett an das bewegte System zurückgegeben, so dass der Rest des Kurvenverlaufs wieder eine horizontale Gerade ist.

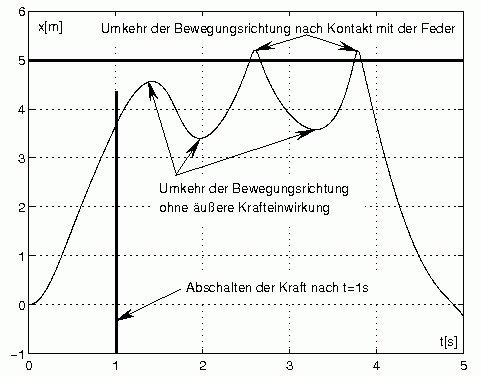
Die nachfolgende Abbildung links zeigt einen Zoom in das Bewegungsgesetz der Laufkatze, der den besonders interessanten Teil der Bewegung verdeutlicht. Was im Diagramm noch etwas überraschend erscheint, wird mit der unten rechts zu sehenden Animation der Bewegung verständlich: Man sieht, wie die schwingende Last auf die Laufkatze einwirkt und Änderungen der Bewegungsrichtung auch ohne äußere Krafteinwirkung erzwingt:

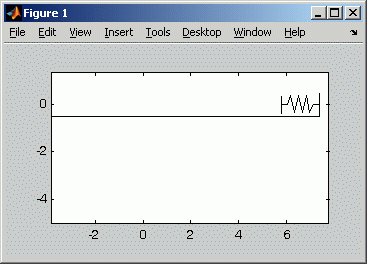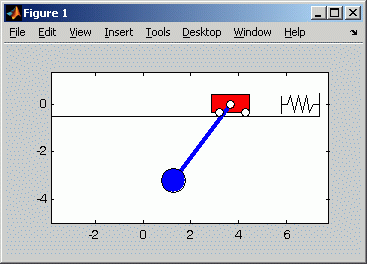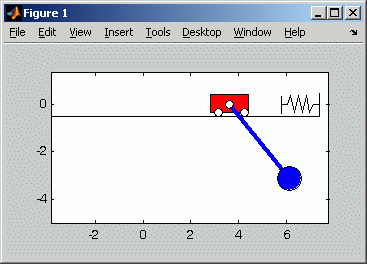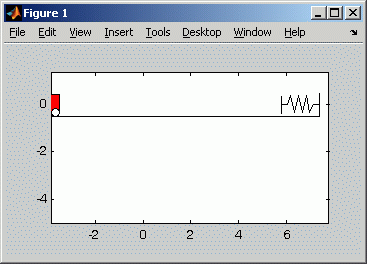
Die Animation zeigt die Bewegung von Laufkatze und Last etwa für den Zeitbereich, der im links zu sehenden Diagramm als Bewegungsgesetz der Laufkatze dargestellt ist.

Sinn und Notwendigkeit von Kontrollfunktionen

Die Auswirkungen zu großer Schrittweiten bei der numerischen Integration von Anfangswertproblemen zeigt die nebenstehende Graphik. Sie ist das Ergebnis einer Rechnung mit nur 50 Runge-Kutta-Schritten.

Bei den beiden Bewegungsgesetzen für Laufkatze und pendelnde Last würde man keinen Verdacht schöpfen, im Gegenteil: Dass die Laufkatze genau einmal an die Feder anschlägt und dann ihren Rückweg antritt, entspricht eigentlich den Erwartungen.

Aber die Funktion T_ges(t) zeigt einen unmöglichen Verlauf: Nachdem sich die Laufkatze nach ihrem Anschlag an die Feder wieder von dieser gelöst hat, ist die Energie des bewegten Systems plötzlich viel größer als vor dem Anschlag. Auch der weitere Verlauf der Kurve, der eine horizontale Gerade sein müsste, zeigt, dass diese Rechnung falsch sein muss.

Download

Das oben zu sehende Matlab-Script steht als LaufkatzeRK4.m zum Download zur Verfügung, ebenso die im dem Script aufgerufene Function "Runge-Kutta 4. Ordnung" als rk4.m.