Aufgabe: Ein dünner Stab der Länge l mit konstantem Querschnitt ist an einem Ende reibungsfrei gelagert. Er wird aus der vertikalen Lage um den Winkel φ₀ ausgelenkt und ohne Anfangsgeschwindigkeit freigegeben (Luftwiderstand kann vernachlässigt werden).

Gegeben:  l = 1 m ;  Erdbeschleunigung g = 9,81 m/s² ,  φ₀ = 3π/4.

Es sind die Bewegungsgesetze φ(t) und ω(t) für die ersten 10 Sekunden der Bewegung zu ermitteln.

Im Kapitel "Kinetik starrer Körper" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird das Anfangswertproblem für diese Aufgabe hergeleitet:

Vorbereitung der Matlab-Rechnung

Mit den ode-Funktionen von Matlab können Differenzialgleichungssysteme 1. Ordnung gelöst werden. Deshalb wird durch Einführen einer zusätzlichen abhängigen Variablen ω aus der Differenzialgleichung 2. Ordnung ein Differenzialgleichungssystem 1. Ordnung:

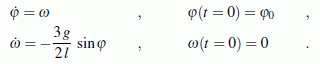
Nachfolgend wird der "Standard-Solver" für Anfangswertprobleme in MATLAB ode45 verwendet (MATLAB-Help: "When to use ode45? Most of the time."). Mit

[T,Y] = ode45(odefun,tspan,y0)

wird ein System von gewöhnlichen Differenzialgleichungen (ordinary differential equations) gelöst, die in der Funktion odefun(t,y) definiert sein müssen. tspan ist das Intervall, über das integriert werden soll, y0 der Vektor der Anfangsbedingungen.

Die Funktion ode45 arbeitet mit variabler Schrittweite und liefert einen Vektor T und eine Matrix Y ab. T enthält alle Zeitpunkte des Intervalls (einschließlich Anfangs- und Endpunkt), für die Ergebnisse berechnet wurden, Y spaltenweise die zugehörigen Ergebnisse.

MATLAB-Help gibt Auskunft über den Lösungsalgorithmus: "ode45 is based on an explicit Runge-Kutta (4,5) formula, the Dormand-Prince pair" (vgl. Skript "Numerische Integration von Anfangswertproblemen").

Matlab-Script

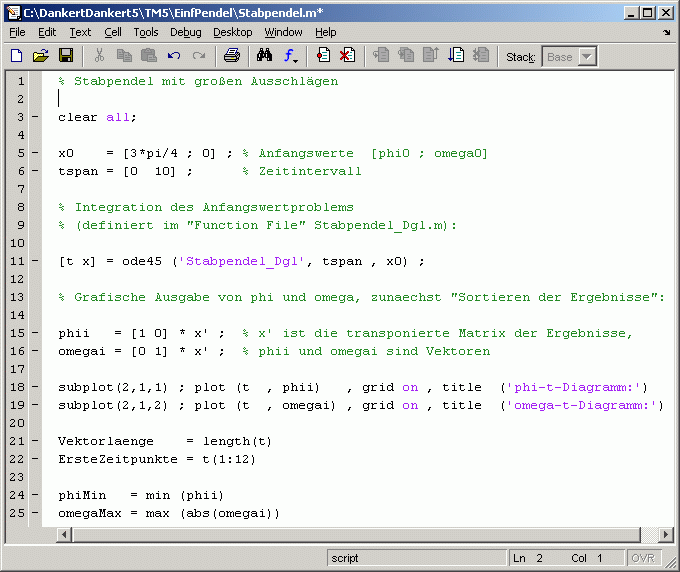
Für das aktuelle Problem mit zwei zu ermittelnden Funktionen (phi und omega) und damit zwei Differenzialgleichungen muss ein Spaltenvektor mit zwei Anfangswerten definiert werden (Zeile 5 in der nebenstehend zu sehenden M-Datei). In Zeile 6 wird das Zeitintervall, für das die Lösung gesucht wird, als Zeilenvektor definiert.

Beide Vektoren werden (neben dem Namen der Funktions-Datei, in der die Differenzialgleichungen definiert werden) der Funktion ode45 übergeben. Die Funktion liefert in der 1. Spalte der Matrix x alle berechneten phi-Werte und in der 2. Spalte alle berechneten omega-Werte ab. Sie beziehen sich auf die Zeitpunkte, die im Vektor t abgeliefert werden.

In den Scriptzeilen 15 und 16 werden die Ergebnisse auf separate Vektoren (durch Multiplikation der transponierten Ergebnis-Matrix mit Einheitsvektoren) übertragen, die in den Scriptzeilen 18 und 19 über der Zeit graphisch dargestellt werden.

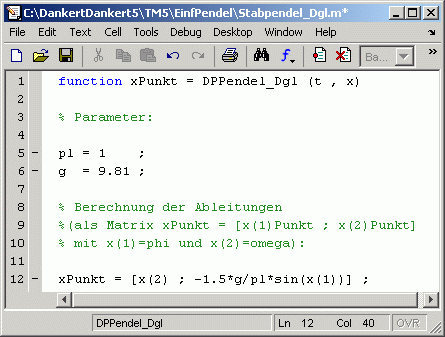Die nebenstehend zu sehende Funktion Stabpendel_Dgl definiert die beiden Differenzialgleichungen:

Eingangswerte sind ein Zeitpunkt t (einfache Variable) und die Funktionswerte zu diesem Zeitpunkt im Vektor x (phi als x(1) und omega als x(2)). Abgeliefert wird ein Spaltenvektor xPunkt mit den beiden berechneten Ableitungen. In Zeile 14 ist die Berechnung der Ableitungen zu sehen: Das erste Element x(2) entspricht der ersten Differenzialgleichung phiPunkt=omega, das zweite Element 1.5*g/pl*sin(x(1)) entspricht der zweiten Differentialgleichung omegaPunkt=1.5*g/pl*sin(x(1)).

Ergebnisse

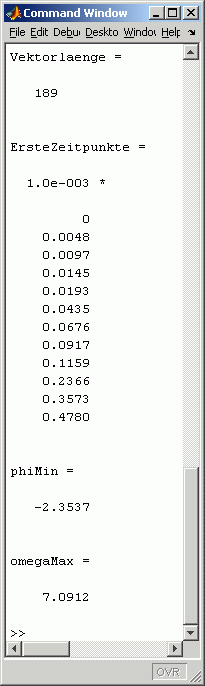
Nach Abarbeitung des Scripts Stabpendel.m erscheint in einem separaten Fenster die grafische Ausgabe der berechneten Funktionsverläufe (Bild unten).

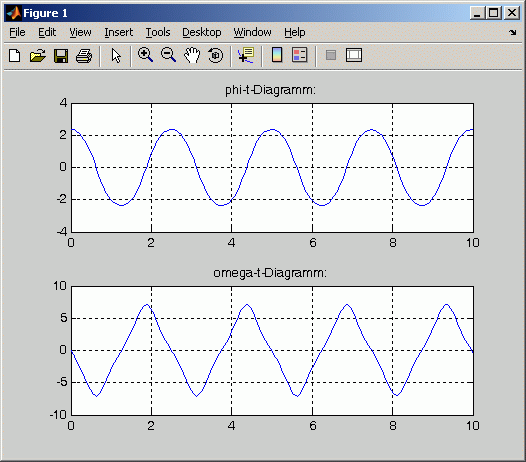
Im Command Window (rechts) sieht man, dass das Zeitintervall t = 0 ... 10 in 188 Abschnitte unterteilt wurde, weil der Vektor t 189 Elemente enthält, von denen die ersten 12 auch gelistet wurden. Die variable Schrittweite des Integrationsprozesses wird deutlich: Während ode45 mit der sehr kleinen Schrittweite 0,0048 beginnt (das ist sinnvoll, denn die Anfangsfehler haben besonderen Einfluss auf die weitere Rechnung), wächst diese sehr schnell auf 0,1207 an.

Die ausgegebenen Werte phiMin und omegaMax dienen der Kontrolle der Qualität der Rechnung. Weil die Schwingung aus der Lage phi = 3π/4 = 2,3562) beginnt und reibungsfrei abläuft, müsste das Pendel in der anderen Richtung um phi = −2,3562 ausschlagen. Die maximale Winkelgeschwindigkeit tritt jeweils in der tiefsten Lage auf und kann mit dem Energiesatz leicht berechnet werden (man erhält: ω_max = 7,08803 s^-1).

Verbesserung der Genauigkeit

Natürlich liegen die Abweichungen der oben berechneten Ergebnisse in akzeptablen Grenzen, aber die grundsätzlichen Warnungen gelten auch für die numerische Integration von Anfangswertproblemen mit Matlab (auch bei Verwendung der anderen "Solver", die Matlab anbietet). Die (in ode45 realisierte) automatische Schrittweitensteuerung kann in der Regel nur lokal steuern (bemerkt also, wenn ein bestimmter Integrationsschritt kritisch ist). Die Empfehlung der Doppelrechnung mit unterschiedlichen Schrittweiten über das gesamte Intervall oder gleichwertige Vorsichtsmaßnahmen gilt also auch hier.

Matlab bietet dafür geeignete Optionen an, die man dem Solver (hier ode45) als zusätzlichen Parameter übergibt. Relativ einfach zu realisieren ist die "MaxStep"-Option (MATLAB-Help: "Positive scalar, an upper bound on the magnitude of the step size that the solver uses. The default is one-tenth of the tspan interval."). Die Optionen werden mit der Funktion odeset gesetzt. Für das behandelte Problem könnte dies z. B. so aussehen:

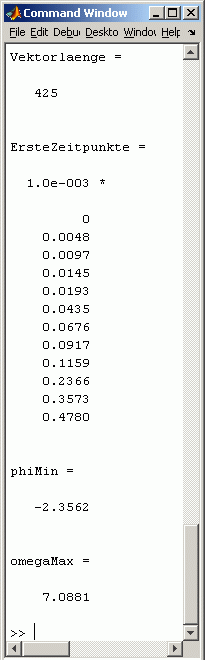
In der Scriptzeile 10 wird die "MaxStep"-Option auf den Wert 0,1 gesetzt, die Struktur options wird der Funktion ode45 als vierter Parameter angeboten. Dies hat zur Folge, dass das Integrationsintervall in 424 Abschnitte unterteilt wird, die damit berechneten Ergebnisse sind praktisch exakt (Bild rechts).

Die oben gelistetem M-Dateien sind als Stabpendel.m bzw. Stabpendel_Dgl.m zum Download verfügbar.

Auch in Matlab gilt für die numerische Integration von Anfangswertproblemen, dass Kontrollrechnungen unabdingbar sind. Mit den Standard-Einstellungen kann die gewünschte Genauigkeit unter Umständen nicht erreicht werden (im aktuellen Beispiel waren die Auswirkungen marginal und damit vertretbar, das ist aber durchaus nicht immer der Fall). Es ist aber auch durchaus möglich, dass die Abweichungen von der exakten Lösung nach einer gewissen Integrationsstrecke zu völlig falschen Ergebnissen führen. Die recht einfache Aufgabe als Einstieg in die numerische Integration von Anfangswertproblemen ist dafür ein markantes Beispiel.