
|
Doppelpendel - Berechnung mit Matlab
|
 Achtung, hier wird geschummelt!
Achtung, hier wird geschummelt!
|
|||||
|
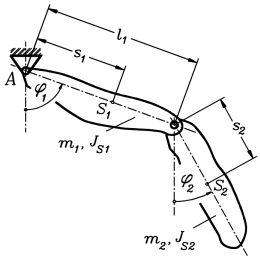
Aufgabe
Ein Doppelpendel wird definiert durch die beiden Pendelmassen m1 und m2, die auf die jeweiligen Schwerpunkte bezogenen Massenträgheitsmomente JS1 und JS2, die Schwerpunktabstände von den Drehpunkten s1 und s2 und den Abstand l1 der beiden Drehpunkte voneinander.
Die Bewegung soll durch die Funktionen φ1(t) und φ2(t) beschrieben werden, die für das Zeitintervall t = 0 ... 10 s zu berechnen sind.
Die Aufgabe wird in den Kapiteln "Prinzipien der Mechanik" und "Verifizieren von Computerrechnungen" behandelt.
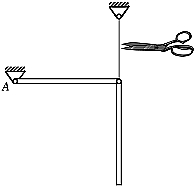
Die gegebenen Werte gelten für zwei schlanke Stäbe gleicher Masse und gleicher Länge. Sie sollen aus der nebenstehend skizzierten Anfangslage ohne Anfangsgeschwindigkeiten freigelassen werden, so dass folgende Anfangsbedingungen gelten:
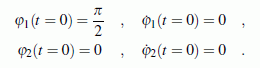
Bewegungs-Differenzialgleichungen, Vorbereitung der Matlab-Rechnung
Unter Verwendung der in der Aufgabenstellung skizzierten Koordinaten gelten folgende Bewegungs-Differenzialgleichungen (die ausführlich kommentierte Herleitung findet man im Kapitel "Prinzipien der Mechanik"):
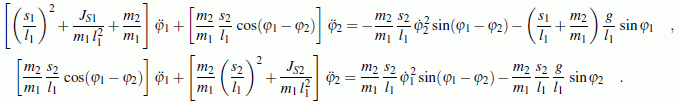
Die Matlab-Solver für die numerische Integration erwarten ein Differenzialgleichungssystem 1. Ordnung. Deshalb werden die beiden neuen Variablen ω1 und ω2 eingeführt:
Damit kann das Anfangswertproblem so formuliert werden, wie man es Matlab anbieten kann:
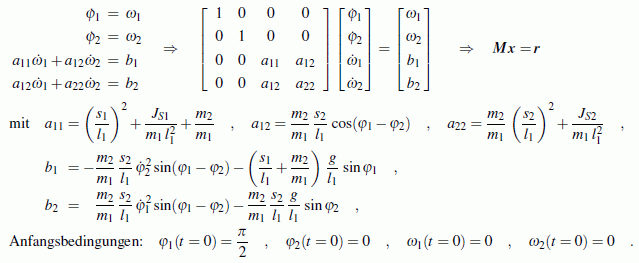
Matlab-Script
Weil das Bewegungs-Differenzialgleichungssystem in den Beschleunigungsgliedern gekoppelt ist, entsteht nach dem Umschreiben auf ein System 1. Ordnung auf der linken Seite des Differenzialgleichungssystems eine "Massenmatrix" M. Matlab kann damit umgehen, man muss nur über die "options", die dem Solver (hier: ode45) übergeben werden, ankündigen, dass eine gesonderte Function diese Matrix beschreibt (hier wird für diese Function der Name Massenmatrix gewählt).
Die beiden Functions, mit denen das Differenzialgleichungssystem definiert wird (hier willkürlich Massenmatrix und RechteSeite genannt) empfangen die gleichen Werte: Zeit t und Vektor der Funktionswerte mit φ1(t), φ2(t), ω1(t), ω2(t), so dass gemeinsam mit den gegebenen Parametern der Aufgabenstellung alle Informationen verfügbar sind, um die aktuelle Massenmatrix und die aktuelle rechte Seite des Differenzialgleichungssystems zu berechnen und abzuliefern.
Es wird der Matlab-Standard-Solver ode45 verwendet. Weil keine weiteren Maßnahmen vorgesehen sind, um die Ergebnisse zu verifizieren, wird die "MaxStep"-Option vorsichtshalber mit dem relativ kleinen Wert 0.01 belegt, der ausreichend kleine Schrittweiten erzeugen wird. Der Rest des Scripts dürfte selbsterklärend sein:
if nargin == 2 % Start mit vorgegebenen Anfangswerten?
x0 = [phi1Anf ; phi2Anf ; 0 ; 0] ; % Anfangswerte [phi1 ; phi2 ; omega1 ; omega2]
else
x0 = [pi/2 ; 0 ; 0 ; 0] ; % Default-Anfangswerte
end
% Parameter (global definiert, damit Wertaenderung nur an einer Stelle erforderlich):
global mdm J1 J2 s1 s2 gdl
mdm = 1 ; J1 = 1./12 ; J2 = 1./12 ; s1 = .5 ; s2 = .5 ; gdl = 9.81 ;
tspan = [0 ; 10] ; % Zeitintervall
% Integration des Anfangswertproblems:
options = odeset('Mass' , @Massenmatrix , 'MaxStep' , 0.01) ;
[t xv] = ode45 (@RechteSeite , tspan , x0 , options) ;
% Grafische Ausgabe von phi1 und phi2, zunaechst "Sortieren der Ergebnisse":
phi1 = xv(:,1) ;
phi2 = xv(:,2) ; % phi1i und phi2i sind Vektoren
subplot(2,1,1) ; plot (t , phi1) , grid on , title ('\phi_1(t) (oberes Pendel)')
subplot(2,1,2) ; plot (t , phi2) , grid on , title ('\phi_2(t) (unteres Pendel)')
% ============================================================
% Funktion, die die "Massenmatrix" des Dgl.-Systems definiert:
function M = Massenmatrix (t , xv)
global mdm J1 J2 s1 s2 gdl
phi1 = xv(1) ;
phi2 = xv(2) ;
omega1 = xv(3) ;
omega2 = xv(4) ;
c = cos(phi1-phi2);
M = [ 1 0 0 0 ;
0 1 0 0 ;
0 0 s1^2+J1+mdm mdm*s2*c ;
0 0 mdm*s2*c mdm*s2^2+J2 ] ;
% ============================================================
% Funktion, die die "rechte Seite" des Dgl.-Systems definiert:
function xvp = RechteSeite (t , xv)
global mdm J1 J2 s1 s2 gdl
phi1 = xv(1) ;
phi2 = xv(2) ;
omega1 = xv(3) ;
omega2 = xv(4) ;
s = sin(phi1-phi2);
phi1p = omega1 ;
phi2p = omega2 ;
omega1p = -mdm*s2*omega2^2*s - (s1+mdm)*gdl*sin(phi1) ;
omega2p = mdm*s2*omega1^2*s - mdm*s2*gdl*sin(phi2) ;
xvp = [phi1p ; phi2p ; omega1p ; omega2p] ;
- Zu den hellblauen Zeilen: Die Funktion "DoppelPendel" kann aufgerufen werden mit Angabe der Anfangsauslenkungen der beiden Stäbe oder ohne Parameter. Im letztgenannten Fall werden Default-Werte (das sind die Werte der Aufgabenstellung) verwendet.
- Zur weißen Zeile: Mit der Option "Mass" wird angekündigt, dass eine Massenmatrix zu berücksichtigen ist, der folgende Parameter gibt den Namen der dafür bereitgestellten Funktion an. Die Option "MaxStep" ist zwingend, um über ein Zeitintervall von 10 Sekunden ausreichend genaue Ergebnisse zu erzielen, vgl. hierzu die Seite "Doppelpendel - Matlab (mit Kontrollen)".
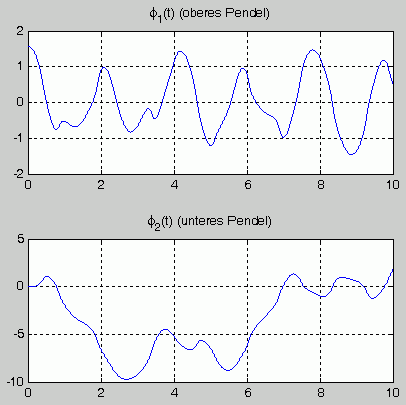
Ergebnisse
Das Matlab-Script liefert die nebenstehend zu sehenden Bewegungsgesetze. Die recht bizarren Funktionsverläufe spiegeln den tatsächlich außerordentlich komplizierten Bewegungsablauf eines solchen Doppelpendels wider. Während das obere Pendel eine recht unregelmäßige Schwingung ausführt, beginnt das untere Pendel mit einem "Salto", dem bald darauf ein "Salto rückwärts" folgt.
Eine etwas bessere Vorstellung vom Bewegungsverlauf liefert die Modifikation des oben gelisteten Scripts, die eine ganz einfache Animation zeigt.
