 |
||||||||||||||||||||||||||||||||||
|
Zur Startseite |
||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
Unter Verwendung der Parameter R = 1 m , μ = 0,05 , g = 9,81 m/s2 soll für den Zeitbereich 0 ≤ t ≤ 10 s folgendes Anfangswertproblem gelöst werden: |
||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||
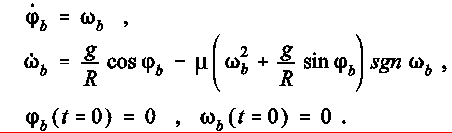 |
||||||||||||||||||||||||||||||||||
|
Nachfolgend wird der “Standard-Solver” für Anfangswertprobleme in Matlab ode45 verwendet (Matlab-Help: “When to use ode45? Most of the time.”). Mit [T,Y] = ode45(odefun,tspan,y0) wird ein System von gewöhnlichen Differenzialgleichungen (ordinary differential equations) gelöst, die in der Funktion odefun(t,y) definiert sein müssen. tspan ist das Intervall, über das integriert werden soll, y0 der Vektor der Anfangsbedingungen. Die Funktion ode45 liefert einen Vektor T und eine Matrix Y ab. T enthält alle Zeitpunkte des Intervalls (einschließlich Anfangs- und Endpunkt), für die Ergebnisse berechnet wurden, Y spaltenweise die zugehörigen Ergebnisse. Matlab-Help gibt Auskunft über den Lösungsalgorithmus: “ode45 is based on an explicit Runge-Kutta (4,5) formula, the Dormand-Prince pair”. Das Verfahren von Dormand-Price ist ein Runge-Kutta-Verfahren fünfter Ordnung, das in jedem Schritt zwei Approximationen berechnet, die für eine lokale Fehlerabschätzung genutzt werden. Im Gegensatz zu den klassischen Runge-Kutta-Formeln werden 7 statt nur 4 “k-Werte” berechnet, aus denen je eine Approximation 4. bzw. 5. Ordnung gebildet werden. Mit zwei Zwischenergebnissen in jedem Schritt kann dann eine (lokale) Fehlerabschätzung durchgeführt werden, die für eine Schrittweitensteuerung genutzt werden kann. |
||||||||||||||||||||||||||||||||||
|
Beide Vektoren werden (neben dem Namen der Funktions-Datei, in der die Differenzialgleichungen definiert werden) der Funktion ode45 übergeben. Die Funktion liefert in der 1 . Spalte der Matrix x alle berechneten phi-Werte und in der 2. Spalte alle berechneten omega-Werte ab. Sie beziehen sich auf die Zeitpunkte, die im Vektor t abgeliefert werden. In den Scriptzeilen 13 und 14 werden die Ergebnisse auf separate Vektoren (durch Multiplikation der transponierten Ergebnis -Matrix mit Einheitsvektoren) übertragen, die in den Scriptzeilen 16 und 17 über der Zeit graphisch dargestellt werden.
Eingangswerte sind ein Zeitpunkt t (einfache Variable) und die Funktionswerte zu diesem Zeitpunkt im Vektor x (phi als x(1) und omega als x(2)). Abgeliefert wird ein Spaltenvektor xPunkt mit den beiden berechneten Ableitungen. In Zeile 12 ist die Berechnung der Ableitungen zu sehen: Das erste Element “x(2)” entspricht der ersten Differentialgleichung “phiPunkt=omega”, das zweite Element “g/R*cos(x(1))-...” entspricht der zweiten Differentialgleichung “omegaPunkt=g/R*cos(phi)-...”.
Um zu bestätigen, dass die numerische Rechnung über den Integrationsbereich “gesund” ist, wird die Rechnung mit mu=0 (Änderung der Zeile 7 in S500_Dgl.m) wiederholt, weil bei Reibungsfreiheit der Massenpunkt bei jeder Schwingung die Ausgangshöhe wieder erreichen muss. Das rechte Bild als Ergebnis dieser Rechnung lässt erkennen, dass offensichtlich sowohl Anfangslage als auch die Endlage (φ = π) stets wieder erreicht werden. |
||||||||||||||||||||||||||||||||||
|
Es ist durchaus interessant, wie fein ode45 das Integrationsintervall unterteilt. Die beiden zusätzlichen Zeilen in S500.m
führen zu einer entsprechenden Ausgabe im “Command Window”.
Es ist in jedem Fall empfehlenswert, die beiden Anweisungen
am Ende des Matlab-Scripts einzufügen. Obwohl die Dormand-Prince-Formeln den Anspruch hoher Genauigkeit haben und die damit mögliche Schrittweitensteuerung eine gewisse Sicherheit bringt, sollte mindestens eine zweite Rechnung mit feinerer Schrittweite durchgeführt werden. Matlab bietet dafür geeignete Optionen an, die man dem Solver (hier ode45) als zusätzlichen Parameter übergibt. Relativ einfach zu realisieren ist die “MaxStep”-Option (Matlab-Help: “Positive scalar, an upper bound on the magnitude of the step size that the solver uses. The default is one-tenth of the tspan interval.” Die Optionen werden mit der Funktion odeset gesetzt. Für das behandelte Problem könnte dies z. B. so aussehen:
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
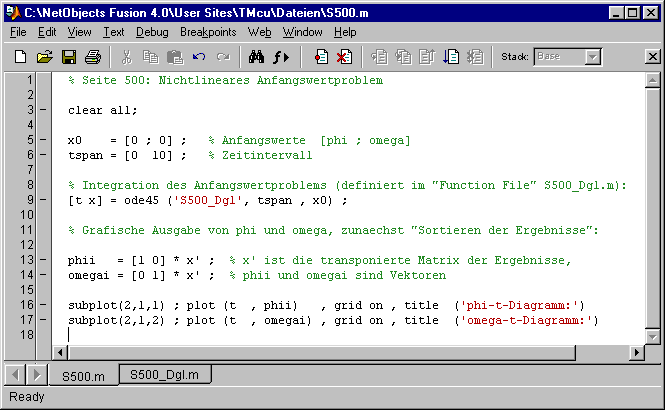 Für das aktuelle Problem mit zwei zu ermittelnden
Funktionen (phi und omega) und damit zwei Differenzialgleichungen muss ein Spaltenvektor mit zwei Anfangswerten definiert werden (Zeile 5 in der nebenstehend zu sehenden m-Datei). In Zeile 6 wird das Zeitintervall, für das die
Lösung gesucht wird, als Zeilenvektor definiert.
Für das aktuelle Problem mit zwei zu ermittelnden
Funktionen (phi und omega) und damit zwei Differenzialgleichungen muss ein Spaltenvektor mit zwei Anfangswerten definiert werden (Zeile 5 in der nebenstehend zu sehenden m-Datei). In Zeile 6 wird das Zeitintervall, für das die
Lösung gesucht wird, als Zeilenvektor definiert.
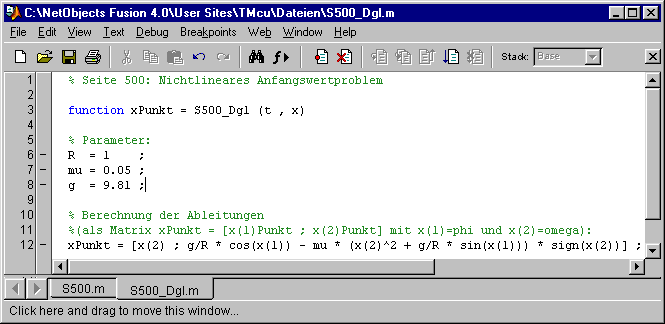 Die nebenstehend zu sehende Funktion S500_Dgl definiert die beiden Differenzialgleichungen:
Die nebenstehend zu sehende Funktion S500_Dgl definiert die beiden Differenzialgleichungen:
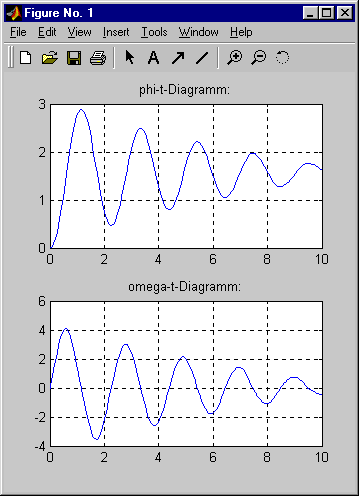
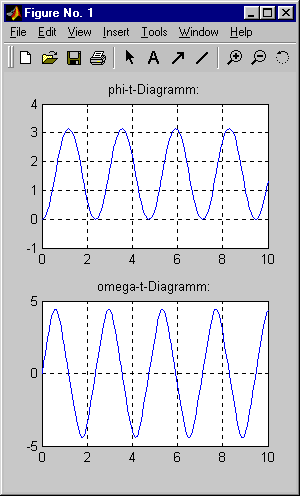 Nach Abarbeitung des Scripts S500.m erscheint in einem separaten Fenster
die graphische Ausgabe der berechneten Funktionsverläufe (Bild links).
Nach Abarbeitung des Scripts S500.m erscheint in einem separaten Fenster
die graphische Ausgabe der berechneten Funktionsverläufe (Bild links).
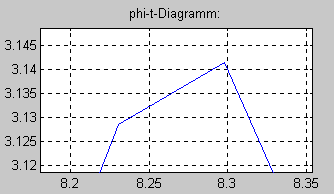 Ein “sehr scharfer Zoom” in den Bereich des letzten Maximalausschlages
verdeutlicht, dass einerseits die berechnete Fuktion natürlich nur ein Polygon ist, andererseits der Wert φ =π tatsächlich sehr genau getroffen wird.
Ein “sehr scharfer Zoom” in den Bereich des letzten Maximalausschlages
verdeutlicht, dass einerseits die berechnete Fuktion natürlich nur ein Polygon ist, andererseits der Wert φ =π tatsächlich sehr genau getroffen wird.
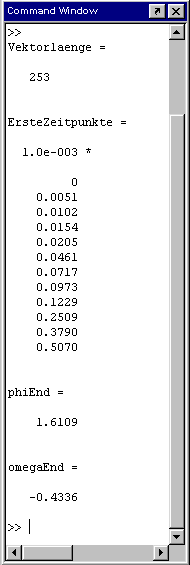 Man erkennt (Bild rechts), dass das Zeitintervall t = 0 .. 10 in 252 Abschnitte unterteilt wird, so
dass der Vektor t 253 Elemente enthält, von denen die ersten 12 auch gelistet wurden. Die variable Schrittweite des Integrationsprozesses wird deutlich: Während ode45 mit der sehr kleinen
Schrittweite 0,0000051 beginnt (das ist sinnvoll, denn die Anfangsfehler haben besonderen Einfluss auf die weitere Rechnung), wächst diese sehr schnell auf 0,000128 an und wird sich noch
wesentlich vergrößern, denn bei 252 Schritten ist die “mittlere Schrittweite” immerhin 10/252 = 0,03968.
Man erkennt (Bild rechts), dass das Zeitintervall t = 0 .. 10 in 252 Abschnitte unterteilt wird, so
dass der Vektor t 253 Elemente enthält, von denen die ersten 12 auch gelistet wurden. Die variable Schrittweite des Integrationsprozesses wird deutlich: Während ode45 mit der sehr kleinen
Schrittweite 0,0000051 beginnt (das ist sinnvoll, denn die Anfangsfehler haben besonderen Einfluss auf die weitere Rechnung), wächst diese sehr schnell auf 0,000128 an und wird sich noch
wesentlich vergrößern, denn bei 252 Schritten ist die “mittlere Schrittweite” immerhin 10/252 = 0,03968.
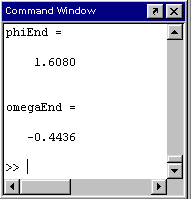
 In der Scriptzeile 9 wird die “MaxStep”-Option auf den (sehr
kleinen) Wert 0,01 gesetzt, die Struktur options wird der Funktion ode45 als vierter Parameter
angeboten. Dies hat zur Folge, dass das Integrationsintervall in 4064 Abschnitte unterteilt wird (linkes Bild), die damit berechneten Ergebnisse (rechtes Bild) sind praktisch exakt.
In der Scriptzeile 9 wird die “MaxStep”-Option auf den (sehr
kleinen) Wert 0,01 gesetzt, die Struktur options wird der Funktion ode45 als vierter Parameter
angeboten. Dies hat zur Folge, dass das Integrationsintervall in 4064 Abschnitte unterteilt wird (linkes Bild), die damit berechneten Ergebnisse (rechtes Bild) sind praktisch exakt.