Differenzenverfahren, Sparse matrix in Matlab

Aufgabe

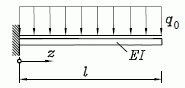
Für den skizzierten Träger mit konstanter Biegesteifigkeit EI ist die Durchbiegung näherungsweise mit dem Differenzenverfahren zu bestimmen.

Gegeben: a ; q₀ ; EI = konstant .

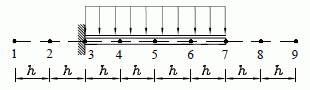
Im Kapitel "Computer-Verfahren für Biegeprobleme" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird gezeigt, dass sich bei der (sehr groben) Einteilung des Trägers in nur n_A = 4 Abschnitte (nebenstehende Skizze) folgendes Gleichungssystem mit n = 9 unbekannten Vertikalverschiebungen v₁, ... ,v₉ (einschließlich der "Außenpunkte") ergibt:

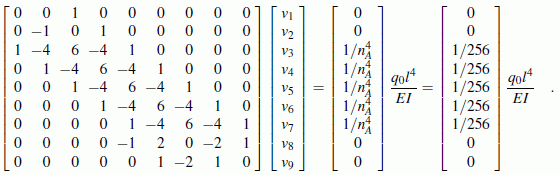
Bei einer feineren Diskretisierung (größerer Wert für n_A) behält das sich dann vergrößernde Gleichungssystem seine grundsätzliche Struktur bei. In der Koeffizientenmatrix gibt es nur mehr Gleichungen vom "1 -4 6 -4 1"-Typ, im Vektor der rechten Seite ändern sich die Zahlenwerte entsprechend dem geänderten n_A. Insgesamt sind es immer n = n_A+5 Gleichungen.

Demonstration der "Sparse Matrix"-Speicherung

Zunächst wird das Gleichungssystem mit 9 Unbekannten (n_A = 4) in einem Matlab-Script erzeugt, um die Speicherung der Koeffizientenmatrix als "Sparse Matrix" zu demonstrieren:

% Differenzenverfahren, Einstiegsbeispiel,
% Koeffizientenmatrix wird als "Sparse Matrix" gespeichert

clear all

ipos = [1 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5 6 6 6 6 6 7 7 7 7 7 8 8 8 8 9 9 9] ;
jpos = [3 2 4 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 5 6 7 8 9 5 6 8 9 6 7 8] ;
AA = [1 -1 1 1 -4 6 -4 1 1 -4 6 -4 1 1 -4 6 -4 1 1 -4 6 -4 1 1 -4 6 -4 1 -1 2 -2 1 1 -2 1] ;

A = sparse (ipos,jpos,AA,9,9) ;

b = [0 ; 0 ; 1/256 ; 1/256 ; 1/256 ; 1/256 ; 1/256 ; 0 ; 0] ;

v = A\b

Die "Sparse Matrix"-Speicherung wird von der Matlab-Function sparse realisiert, der 2 Vektoren mit den Indizes der Nicht-Null-Elemente (im Beispiel: ipos und jpos) und ein Vektor mit den Nicht-Null-Elementen (im Beispiel: AA) angeboten werden müssen. Zwei weitere Parameter sind die Zeilen- und Spaltenanzahl der Matrix. Die miteinander korrespondierenden Indizes und das zugehörige Matrixelement stehen im obigen Beispiel-Script jeweils untereinander, beginnend mit 1,3,1 für die 1 auf der dritten Position in der ersten Zeile.

Nach dem Abarbeiten des Scripts S261Sparse1.m findet man das Ergebnis im "Command Window" (Bild rechts).

"Sparse Matrix"-Speicherung für beliebig große Matrizen

Das folgende Script S261Sparse2.m zeigt die Definition des beliebig großen Gleichungssystems in den hellblauen Zeilen. Die Möglichkeit unterschiedlich feiner Unterteilung des Trägers wird nur über die Angabe des Wertes für nA (in der weißen Zeile am Anfang) gesteuert.

% Differenzenverfahren, Beispiel auf den Seiten 260 bis 262,
% Koeffizientenmatrix wird als "Sparse Matrix" gespeichert

clear all

L = 1 ;
q0 = 1 ;
EI = 1 ;
nA = 1000   ; % Anzahl der Abschnitte (nur dieser Wert muss geaendert werden)
n = nA + 5 ; % Anzahl der Gleichungen
h = L / nA ;

nRBlinks = 3 ; % 3 Werte fuer Beschreibung der Einspannung
nRBrechts = 7 ; % 4 Werte fuer Beschreibung des freien Randes
nspare = (n-4)*5+nRBlinks+nRBrechts ;
AA = zeros (nspare,1) ;
ipos = zeros (nspare,1) ;
jpos = zeros (nspare,1) ;
b = zeros (n ,1) ;

%Einspannung links:
ipos(1:3) = [1 2 2] ;
jpos(1:3) = [3 2 4] ;
AA (1:3) = [1 -1 1] ;

ii = nRBlinks+1 ;
for i=3:n-2 % Matrix A:
   ipos(ii:ii+4) = i ;
   jpos(ii:ii+4) = i-2:i+2 ;
   AA (ii:ii+4) = [1 -4 6 -4 1] ;
   b (i) = q0*h^4/EI ;
   ii=ii+5 ;
end

% Freier Rand rechts:
ipos(ii:ii+6) = [n-1 n-1 n-1 n-1 n n n ] ;
jpos(ii:ii+6) = [n-4 n-3 n-1 n n-3 n-2 n-1] ;
AA (ii:ii+6) = [ -1 2 -2 1 1 -2 1 ] ;

A = sparse (ipos,jpos,AA,n,n) ;

t1 = cputime ;
v = A \ b ; % Loesen des Gleichungssystems (Berechnung der Durchbiegung v)
ZeitGlSyst = cputime - t1

format long
vEnd = v(n-2)
phiEnd = (-v(nA+2) + v(nA+4)) / (2*h)
Mblinks = -EI/h^2 * (v(2) - 2*v(3) + v(4))

for i = 3:n-2
   Mb(i) = - EI/h^2 * (v(i-1) - 2*v(i) + v(i+1)) ;
end

z = 0 : h : L ;
subplot (2 , 1 , 1) ; plot (z , v (3:n-2)) , axis ij , title ('Verschiebung')
subplot (2 , 1 , 2) ; plot (z , Mb(3:n-2)) , title ('Biegemoment')

Nach der Lösung des Gleichungssystems werden mit den Zeilen, die nicht mit einem Semikolon abgeschlossen sind, neben der für die Lösung verbrauchten Zeit drei Ergebnisse in das "Command Window" ausgegeben: Verschiebung am Trägerende und der Biegewinkel an dieser Stelle, der mit Hilfe der Differenzenformel für die erste Ableitung aus den Verschiebungen der beiden Nachbarpunkte berechnet wird, sowie das auf entsprechende Weise mit der Näherung der zweiten Ableitung berechnete Biegemoment an der Einspannung. Schließlich wird in einer Schleife der gesamte Biegemomentenverlauf berechnet, und Durchbiegung und Biegemomentenverlauf werden in ein Graphik-Fenster gezeichnet. Für die oben gelistete Datei (mit nA = 1000, Gleichungssystem mit 1005 Gleichungen) sehen nach der Berechnng das "Command Window" und das Graphik-Fenster so aus:

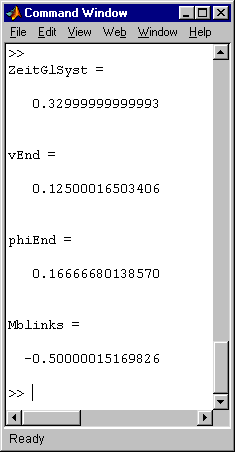
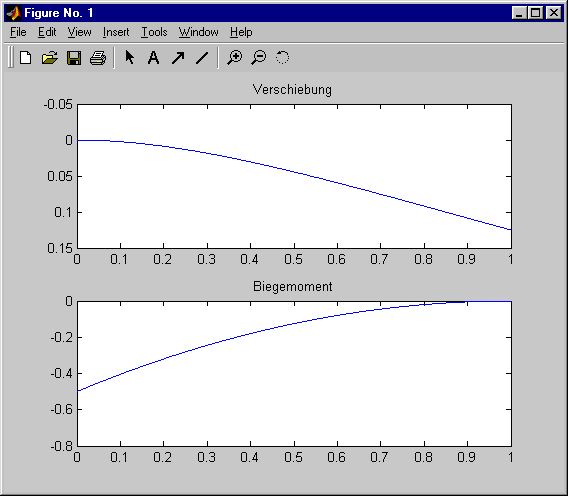
Um die Aufgabe für unterschiedlich feine Diskretisierung zu berechnen, muss in der oben gelisteten m-Datei jeweils nur der Wert für nA geändert werden.