
- Lösung mit dem Differenzenverfahren -
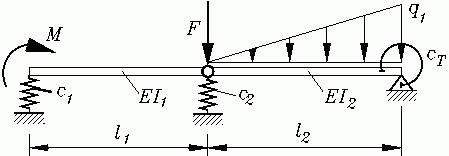
Aufgabe
Für den skizzierten Träger sollen die Biegelinie, der Biegemomentenverlauf und der Querkraftverlauf berechnet werden (Aufgabe aus dem Kapitel "Computerverfahren für Biegeprobleme").
Gegeben:
l1 = 1200 mm ;
EI1 = 2,5 kNm2 ;
c1 = 50 N/mm ;
l2 = 1300 mm ;
EI2 = 5 kNm2 ;
c2 = 250 N/mm ;
cT = 5 kNm ;
q1 = 1,3 N/mm ;
F = 800 N ;
M = 250 Nm .
Lösung mit dem Differenzenverfahren
Die Rechnung wird mit dem nachfolgend gelisteten Matlab-Script durchgeführt, in dem das Gleichungssystem für das Differenzenverfahren aufgebaut und gelöst werden. Die Strategie folgt den Empfehlungen, die im Kapitel "Computer-Verfahren für Biegeprobleme" gegeben und im Kapitel "Spezielle Biegeprobleme" verallgemeinert wird. Die Ergebnisse werden graphisch dargestellt, ausgewählte Zahlenwerte werden in das Command Window ausgegeben:
% Berechnung mit dem Differenzenverfahren
clear all
L1 = 1200 ;
L2 = 1300 ;
EI1 = 2.5e9 ;
EI2 = 5e9 ;
c1 = 50 ;
c2 = 250 ;
cT = 5e6 ;
q1 = 1.3 ;
F = 800 ;
M = 250000 ;
L = L1+L2 ; % Laenge
EIB = EI1 ; % Bezugs-Biegesteifigkeit
nA = 2500 ; % Anzahl der Abschnitte
n = nA + 5 ; % Anzahl der Gleichungen
h = L / nA ; % Schrittweite
A = zeros (n,7) ; % Rechteckmatrix fuer Aufnahme der Bandmatrix
b = zeros (n,1) ; % Nullvektor ("rechte Seite")
qi = zeros (n,1) ; % Linienlastintensitaeten an Stuetzpunkten
mi = zeros (n,1) ; % EIi = mi * EIB
ki = zeros (n,1) ; % Bettungszahlen an Stuetzpunkten
% Markante Punkte (Gelenk und rechter Rand):
iG = round (nA*L1/L + 3) ;
icT = n - 2 ;
% Belastung
qi(iG:icT) = 0 : q1/(icT-iG) : q1 ;
qi(iG) = F/h ;
% Biegesteifigkeit (mue-Werte):
mi(1:iG-1) = EI1/EIB ;
mi(iG) = 0 ;
mi(iG+1:n) = EI2/EIB ;
% Feder c2:
ki(iG) = c2/h ;
%Randbedingungen:
A(1:2,:) = [0 0 0 0 mi(3) -2*mi(3) mi(3) ;
0 0 mi(2) -2*mi(2) mi(2)-mi(4)-2*c1*h^3/(EIB) 2*mi(4) -mi(4)] ;
b(1) = -M*h^2/(EIB) ; % Randbedingungen links: Feder und Moment
A(n-1:n,:) = [0 0 1 0 0 0 0 ;
mi(icT)-cT*h/(2*EIB) -2*mi(icT) mi(icT)+cT*h/(2*EIB) 0 0 0 0] ;
% Lager und Drehfeder rechts
for i = 3:n-2 % Matrix A:
A(i,:)= [0 mi(i-1) -2*(mi(i-1)+mi(i)) mi(i-1)+4*mi(i)+mi(i+1)+ki(i)*h^4/(EIB) ...
-2*(mi(i)+mi(i+1)) mi(i+1) 0] ;
b(i) = qi(i)*h^4/(EIB) ; % Standardgleichungen
end
v = gabamp (A , b) ; % Berechnung der Durchbiegung
clf;
z = 0 : h : L ;
subplot (3,1,1) ; plot (z , v(3:n-2)) , axis ij , grid on ,
title ('Durchbiegung') % Graphische Ausgabe der Biegelinie
for i=3:n-2
Mb(i) = -mi(i)*EIB * (v(i-1)-2*v(i)+v(i+1))/h^2 ; % Biegemoment
FQ(i) = 0.5*EIB * (mi(i-1)*v(i-2)-2*mi(i-1)*v(i-1)+(mi(i-1)-mi(i+1)) ...
*v(i)+2*mi(i+1)*v(i+1)-mi(i+1)*v(i+2))/h^3 ; % Querkraft
end
subplot (3,1,2) ; plot (z , Mb(3:n-2)) , grid on , title ('Biegemoment')
subplot (3,1,3) ; plot (z , FQ(3:n-2)) , grid on , title ('Querkraft')
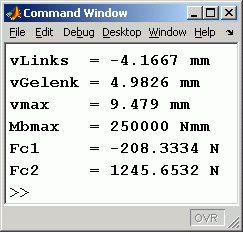
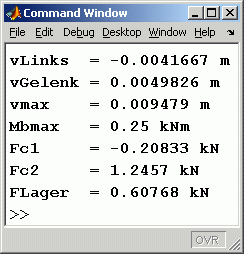
disp (['vLinks = ' , num2str(v(3)), ' mm']) ;
disp (['vGelenk = ' , num2str(v(iG)), ' mm']) ;
disp (['vmax = ' , num2str(max(v(3:n-2))), ' mm']) ;
disp (['Mbmax = ' , num2str(max(Mb(3:n-2))), ' Nmm']) ;
disp (['Fc1 = ' , num2str(c1*v(3)), ' N']) ;
disp (['Fc2 = ' , num2str(c2*v(iG)), ' N']) ;
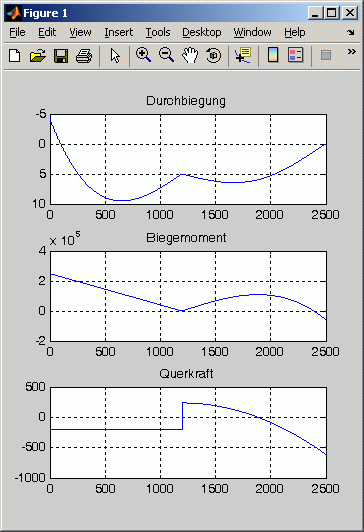
Rechts sieht man die Graphik-Ausgabe des Matlab-Scripts (Biegelinie und Schnittgrößenverläufe).
In das nachstehend zu sehende Command Window wurden einige spezielle Ergebnisse an besonderen Punkten ausgegeben (Absenkung am linken Rand und am Gelenk, maximale Absenkung und maximales Biegemoment, die beiden Federkräfte und die Lagerreaktion am rechten Lager):
Vergleich mit anderen Lösungen
Die gleiche Aufgabe wurde auch analytisch und mit der Finite-Elemente-Methode gelöst. Klicken auf die nachstehenden Bilder führt zu den entsprechenden Seiten:
 Analytische Lösung |
Lösung interaktiv (www.TM-interaktiv.de) mit der Finite-Elemente-Methode |
