Aufgabe

Im Kapitel "Ebene Systeme starrer Körper" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird folgende Aufgabe formuliert:

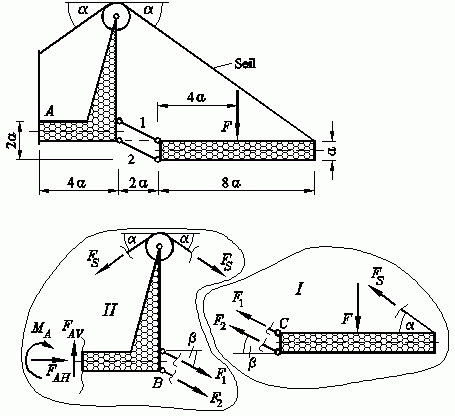
Die skizzierte Arbeitsbühne ist durch die Kraft F belastet. Man ermittle die durch F hervorgerufenen Lagerreaktionen bei A, die Kräfte in den Stäben 1 und 2 und die Seilkraft F_S.

Gegeben:  a ,  F ,  α = 50° .

Entsprechend nebenstehender Schnittskizze lassen sich 6 Gleichgewichtsbedingungen an den beiden Teilsystemen formulieren. Zur Vereinfachung wird der (durch die Abmessungen bekannte) Winkel β eingeführt, der sich aus tan β = a/(2a) = 0,5 berechnen lässt.

Es wird gezeigt, dass sich die Abmessung a aus allen Gleichungen herauskürzt und die Gleichgewichtsbedingungen sich schließlich zu folgendem linearen Gleichungssystem zusammenfassen lassen, in dem die Kraft F als gemeinsamer Faktor auf der rechten Seite steht, so dass auch dafür kein Zahlenwert für eine numerische Lösung erforderlich ist (man muss natürlich alle Ergebnisse mit F multiplizieren):

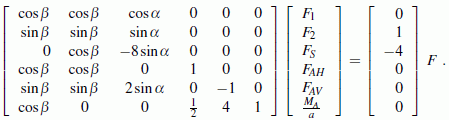
Lösung

Prof. Dr. Barbey macht mit diesem Beispiel darauf aufmerksam, wie elegant die Lösung linearer Gleichungssysteme auch mit MS-Excel (dem Programm, das fast jeder Student auf seinem PC hat) möglich ist.

Rechts ist das Ergebnis der Excel-Rechnung zu sehen.

Der nachfolgende Bildschirm-Schnappschuss zeigt die Formeln, die hinter den einzelnen Zellen liegen. Die hellblau unterlegten Zellen repräsentieren das Gleichungssystem (Matrix A von B13 bis G18, Vektor der rechten Seite von I13 bis I18).

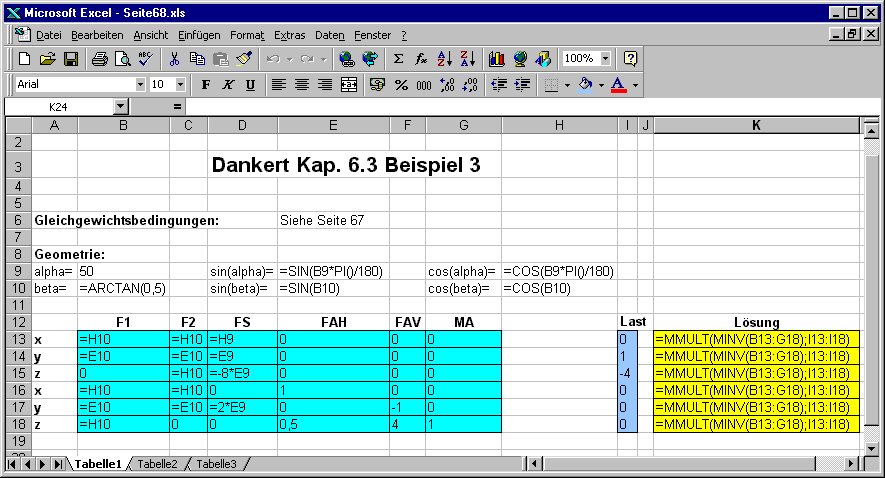
Die Lösung des Gleichungssystems wird von den Formeln in den (gelb unterlegten) Zellen K13 bis K18 realisiert. Die Formel

=MMULT(MINV(B13:G18);I13:I18)

ist zu interpretieren als "Multiplikation (MMULT(...;...)) der Inversen der Matrix A (MINV(B13:G18)) mit dem Vektor der rechten Seite (I13:I18)". Das Ergebnis dieser Multiplikation ist der Vektor der Unbekannten. Wenn das Ergebnis ein (auf mehrere Zellen zu verteilender) Vektor ist, wird die Formel in Excel folgendermaßen eingegeben:

• Markieren der Zellen, die das Ergebnis aufnehmen sollen (in diesem Fall die 6 Zellen I13 bis I18),
• Schreiben der Formel (in diesem Fall: =MMULT(MINV(B13:G18);I13:I18)),
• Eingabe abschließen mir Ctrl+Shift+Return (Strg+Umschalt+Eingabe), die Formel erscheint dann automatisch in allen markierten Zellen.

Zum Download verfügbar: Excel-Datei Seite67.xls.