
Das Problem
Im Kapitel "Systeme mit mehreren Freiheitsgraden" wird darauf aufmerksam gemacht, dass auch für Systeme mit mehreren Freiheitsgraden, die auf ein lineares Differenzialgleichungssystem führen, die Bedürfnisse der technischen Praxis in der Regel erfüllt sind,
- wenn die Lösung des homogenen Differenzialgleichungssystems zur Berechnung der Eigenschwingungen bekannt ist und/oder
- für das inhomogene Differenzialgleichungssystem eine Partikulärlösung gefunden werden kann, die das stationäre Schwingungsverhalten (nach Abklingen der Eigenschwingungen) beschreibt.
Für beide Problemstellung werden im Kapitel "Systeme mit mehreren Freiheitsgraden" mehrere Beispiele demonstriert. Und dann findet man dort noch die Aussage:
Nur für die Beschreibung von Anlaufvorgängen (auch Abbremsen oder Auslaufen) einer Anlage wird die allgemeine Lösung des Systems der Bewegungsdifferenzialgleichungen benötigt. Zur Analyse solcher Vorgänge ist trotz analytischer Lösungsmöglichkeit eine numerische Behandlung meist bequemer.
Das ist noch recht vorsichtig formuliert, denn schon bei kleineren (akademischen) Problemen gilt: Es spricht (fast) nichts gegen die numerische Behandlung, aber vieles (fast alles) gegen die analytische Behandlung. Deshalb wird hier ein kleines Problem gezeigt, das aus der Sicht des Autors dieser Bemerkung schon in die Kategorie fällt: "Lieber gleich numerisch."
Aufgabe
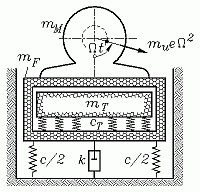
Ein mit der Drehzahl n betriebener Motor ist auf einem elastisch und gedämpft abgestützten Kastenfundament befestigt. Die durch die Motorunwucht U = mu e verursachte Fliehkraft wird in horizontaler Richtung durch die Führung des Fundaments aufgenommen. Die vertikale Komponente kann zu störenden Vertikalschwingungen des Motor-Fundament-Blockes führen, wenn die Erregerkreisfrequenz in der Nähe der Eigenkreisfrequenz des erregten Systems liegt. Deshalb soll ein Tilger im Inneren des Fundaments diese Bewegung tilgen.
- Man berechne die Federzahl cT für den Schwingungstilger (cT soll die resultierende Federzahl der parallel geschalteten Federn zwischen Fundament und Tilger sein).
- Der Einschwingvorgang ist zu analysieren: Man ermittle die Bewegung des Motor-Fundament-Blocks ohne Tilger und mit dem dimensionierten Tilger die Bewegungen von Motor-Fundament-Block und Tilger (t = 0...1,5 s). Anfangsgeschwindigkeiten und -auslenkungen sollen gleich Null angenommen werden.
Gegeben: mM = 50 kg ; mF = 100 kg ; n = 400 min-1 ; c = 2,6·105 N/m ; mT = 75 kg ; mu e = 0,1 kgcm ; k = 3,75·103 kg/s .
Die Aufgabe wurde dem Aufgaben-Pool des Kapitels "Systeme mit mehreren Freiheitsgraden" entnommen.
Diskussion der Lösungsstrategie
Die Fragestellung a ist nach den Regeln für die Schwingungstilgung, die im Kapitel "Systeme mit mehreren Freiheitsgraden" ausführlich behandelt werden (siehe auch dieses Beispiel), problemlos zu erledigen und wird hier nicht betrachtet.
Für Fragestellung b gilt: Die Bewegung ohne Tilger ist eine erzwungene gedämpfte Schwingung mit einem Freiheitsgrad, beschrieben durch die Bewegungs-Differenzialgleichung
Mit dem Tilger wird die erzwungene gedämpfte Schwingung mit zwei Freiheitsgraden durch ein Differenzialgleichungssystem beschrieben:
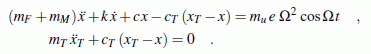
In beiden Fällen zählen die Bewegungskoordinaten jeweils von der statischen Ruhelage der Massen aus und sind nach unten gerichtet positiv. Beide Fälle werden nachfolgend gelöst.
System mit einem Freiheitsgrad: Schwingung ohne Tilger
Für die inhomogene lineare Differenzialgleichung mit konstanten Koeffizienten
kann mit einiger Mühe die allgemeine Lösung ermittelt werden. Es ist die Summe aus der allgemeinen Lösung der homogenen Differenzialggleichung und einer Partikulärlösung der inhomogenen Differenzialgleichung. Dies wird ausführlich beschrieben im Bereich "Mathematik für die Technische Mechanik".
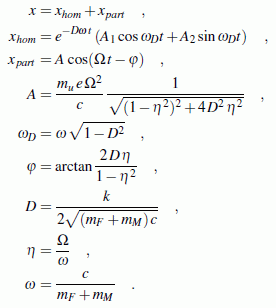
Nebenstehend sind die dort ermittelten Ergebnisse (angepasst an das hier betrachtete Problem) zusammengestellt.
Die allgemeine Lösung der Differenzialgleichung enthält noch die beiden Integrationskonstanten A1 und A2 , die aus den Anfangsbedingungen bestimmt werden:
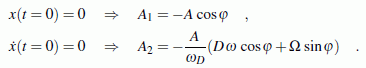
Dieser Formelsatz wird mit dem nachfolgend gelisteten Matlab-Script ausgewertet. Parallel dazu wird die numerische Lösung berechnet. Dafür muss die Differenzialgleichung nur durch Einführen einer zusätzlichen Variablen in ein Differenzialgleichungssystem 1. Ordnung umgewandelt werden:
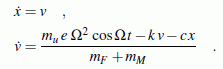
In dem Matlab-Script sind die Passagen, die zur analytischen Lösung gehören, hellblau geschrieben, die zur numerischen Lösung gehörenden Passagen in weiß:
global mM mF mue c k Omega
mM = 50 ; mF = 100 ; mue = 0.1*0.01 ; c = 2.6e5 ; k = 3.75e3 ; n = 400/60 ;
Omega = 2*pi*n ;
x0 = [0 ; 0] ; % Anfangswerte
tspan = [0 1.5] ; % Zeitintervall
% Numerische Integration des Anfangswertproblems:
options = odeset('MaxStep' , 0.01) ;
[t xx] = ode45 (@RechteSeite , tspan , x0 , options) ;
x = xx (:,1) ; % ... numerisch ermitteltes Ergebnis x(t)
% Analytische Lösung:
omega = sqrt(c/(mM + mF)) ;
eta = Omega/omega ;
D = k/(2*sqrt((mM+mF)*c)) ;
phi = atan((2*D*eta)/(1-eta^2)) ;
if (phi < 0) phi = phi+pi ; end
omegaD = omega*sqrt(1-D^2) ;
A = mue*Omega^2/(c*sqrt((1-eta^2)^2+4*D^2*eta^2)) ;
A1 = - A*cos(phi) ;
A2 = - A*(D*omega*cos(phi)+Omega*sin(phi))/omegaD ;
xhom = exp(-D*omega*t).*(A1*cos(omegaD*t)+A2*sin(omegaD*t)) ;
xpart = A*cos(Omega*t-phi) ;
xan = xhom + xpart ; % ... analytisch ermitteltes Ergebnis x(t)
plot (t , xan , t , x) , grid on , title ('x(t), analytische und numerische Lösung')
% ============================================================
% Funktion, die die "rechte Seite" des Dgl.-Systems definiert:
function f = RechteSeite (t , xx)
global mM mF mue c k Omega
x = xx(1) ;
v = xx(2) ;
xp = v ;
vp = (mue*Omega^2*cos(Omega*t) - k*v - c*x)/(mF+mM) ;
f = [xp ; vp] ;
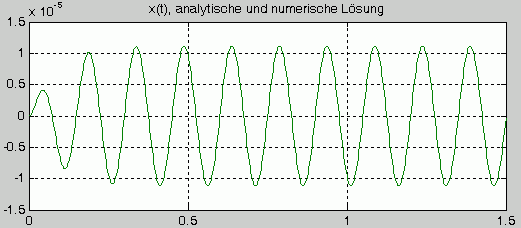
Die beiden Funktionen, die das Script berechnet, werden in ein Graphik-Fenster ausgegeben. Dass die nebenstehend zu sehende Graphik nur eine Kurve zeigt, ist ein sicheres Indiz dafür, dass beide Rechnungen (wie natürlich zu erwarten) zum gleichen Ergebnis führen.
Der Programmieraufwand ist für die beiden Berechnungsverfahren etwa gleich. Der Vorbereitungsaufwand ist allerdings für die analytische Lösung drastisch größer, wie die ausführliche Demonstration der Entwicklung der analytischen Lösung zeigt.
System mit zwei Freiheitsgraden: Schwingung mit Tilger
Das System mit zwei Freiheitsgraden (Fundament und Motor einerseits, Tilgermasse andererseits) wird durch ein lineares inhomogenes Differenzialgleichungssystem 2. Ordnung mit konstanten Koeffizienten beschrieben:
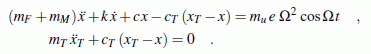
Auch dies ist geschlossen lösbar. Im Kapitel "Systeme mit mehreren Freiheitsgraden" werden zwei Spezialfälle behandelt: Die freien ungedämpften Schwingungen (mu e = 0, k = 0) führen auf ein Matrizeneigenwertproblem, das die beiden Eigenkreisfrequenzen des ungedämpften Systems und die zugehörigen Schwingungsformen (qualitativ) liefert. Für das komplette System wird nur eine Partikulärlösung gesucht, um den stationären Schwingungsverlauf (nach Abklingen der Eigenschwingungen) zu untersuchen. Genau diese beiden Rechnungen liefern die für den Praktiker wichtigen Erkenntnisse.
Um den hier anstehenden Anlaufvorgang zu erfassen, müssten zusätzlich die freien Schwingungen mit Berücksichtigung der Dämpfung erfasst werden, um danach mit dieser Lösung des homogenen Differenzialgleichungssystem und der Partikulärlösung die allgemeine Lösung aufzuschreiben, die dann noch an die Anfangsbedingungen angepasst werden muss. Wenn man sich diesen Weg für das System mit nur einem Freiheitsgrad und die Lösung der beiden Teilprobleme für zwei Freiheitsgrade im Kapitel "Systeme mit mehreren Freiheitsgraden" ansieht, merkt man sehr schnell, dass dieser Versuch nicht empfehlenswert ist, zumal die oben für einen Freiheitsgrad zusätzlich durchgeführte numerische Lösung auf zwei Freiheitsgrade problemlos zu erweitern ist. Das wird hier noch gezeigt.
Vorbereitend wird das Differenzialgleichungssystem 2. Ordnung (2 Gleichungen) durch Einführen von zwei zusätzlichen Variablen in ein Differenzialgleichungssystem 1. Ordnung (4 Gleichungen) umgeschrieben:
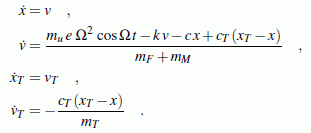
Das nachfolgend gelistete Matlab-Script löst dieses Differenzialgleichungssystem (für die Parameter der Tilgermasse werden die nach Aufgabenstellung a berechneten Werte verwendet, die eine Tilgung der Fundamentschwingungen erwarten lassen). Die (relativ wenigen) Erweiterungen gegenüber dem Script für die Rechnung mit nur einem Freiheitsgrad sind weiß geschrieben:
global mM mF mue c k n Omega mT cT
mM = 50 ; mF = 100 ; mue = 0.1*0.01 ; c = 2.6e5 ; k = 3.75e3 ; n = 400/60 ; mT = 75 ;
Omega = 2*pi*n ;
cT = mT * Omega^2 ;
x0 = [0 ; 0 ; 0 ; 0] ; % Anfangswerte
tspan = [0 1.5] ; % Zeitintervall
% Numerische Integration des Anfangswertproblems:
options = odeset('MaxStep' , 0.01) ;
[t xx] = ode45 (@RechteSeite , tspan , x0 , options) ;
% Grafische Ausgabe, zunaechst "Sortieren der Ergebnisse":
x = xx (:,1) ;
xT = xx (:,3) ;
subplot(2,1,1) ; plot (t , x ) , grid on , title ('x(t): Bewegung des Fundaments')
subplot(2,1,2) ; plot (t , xT) , grid on , title ('x_T(t): Bewegung des Tilgers')
% ============================================================
% Funktion, die die "rechte Seite" des Dgl.-Systems definiert:
function f = RechteSeite (t , xx)
global mM mF mue c k n Omega mT cT
x = xx(1) ;
v = xx(2) ;
xT = xx(3) ;
vT = xx(4) ;
xp = v ;
vp = (mue*Omega^2*cos(Omega*t) - k*v - c*x + cT*(xT-x))/(mF+mM) ;
xTp = vT ;
vTp = -cT*(xT-x)/mT ;
f = [xp ; vp ; xTp ; vTp] ;
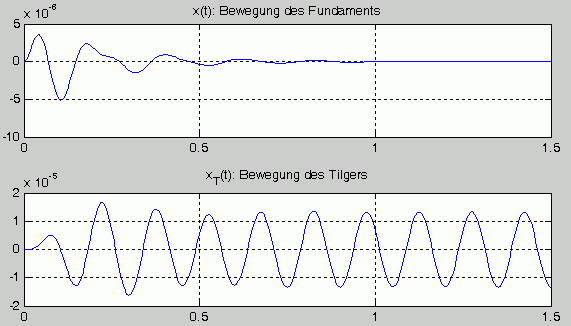
Die nachfolgende Graphik zeigt die Ausgabe des Scripts. Man sieht, dass sich nach einer sehr kurzen Anlaufphase der zu erwartende stationäre Zustand einstellt: Die Fundamentschwingungen werden fast vollständig getilgt, während die Tilgermasse gleichmäßig schwingt.
Download
Die oben zu sehenden Matlab-Scripts stehen als Anlaufvorgang1.m bzw. Anlaufvorgang2.m zum Download zur Verfügung.
