|
|
||||||||||||||||||||||||
|
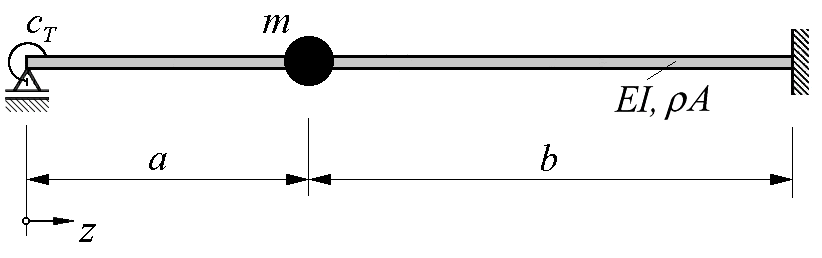
Die Ansatzfunktionen müssen die drei geometrischen Randbedingungen erfüllen (l = a + b):
Das einfachste Polynom, das diese Bedingungen erfüllt, ist das Polynom 3. Grades
Man überzeugt sich leicht, dass auch die höheren Polynomfunktionen
die geometrischen Randbedingungen erfüllen. Das nachfolgend gelistete Matlab-Script arbeitet mit maximal 5 Ansatzfunktionen dieser Art (i = 1 ... 5). Es ist so geschrieben und wird nachfolgend entsprechend kommentiert, dass es als Muster-Script für entsprechende andere Aufgaben dienen kann. Alle gelb eingetragen Zeilen können und sollten für die Lösung anderer Aufgaben unverändert übernommen werden. Zwingend ist nur die Anpassung der drei hellblau geschriebenen Bereiche, die von den Kommentarzeilen der Art % 11111111111 ANPASSEN AN DAS AKTUELLE PROBLEM VON HIER ... 111111111111111111111111111
umschlossen sind. Eine Änderung der grün geschriebene Zeilen kann gegebenenfalls vorgenommen werden, ist aber nicht zwingend.
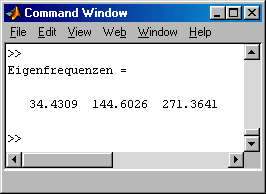
Hier ist es einmal die Drehfeder cT am linken Rand (Punkt 1), die in der Steifigkeitsmatrix ergänzt wird: + cT*vdS(1,ii)*vdS(1,jj). Bei weiteren Drehfedern oder zusätzlichen Federn kommen entsprechende weitere Summanden hinzu, wobei nur die weiß geschriebenen Zeichen modifiziert werden müssen. Während die Drehfederkonstante mit den ersten Ableitungen vdS der Ansatzfunktionen multipliziert werden muss, würde eine der Verschiebung entgegen wirkende Feder mit der Federkonstanten c mit den Verschiebungswerten vS multipliziert werden, eine solche Feder am Punkt kM würde z. B. durch den zusätzlichen Summanden + c*vS(kM,ii)*vS(kM,jj) erfasst werden. Nun muss noch die Einzelmasse am Punkt kM ergänzt werden, die durch einen zusätzlichen Summanden in der Massenmatrix realisiert wird: + mk*vS(kM,ii)*vS(kM,jj). Weitere Einzelmassen würden durch entsprechende zusätzliche Summanden erfasst werden. Der Rest des Scripts beinhaltet die Lösung des Allgemeinen Matrizeneigenwertproblems (vgl. hierzu die Site "Matrizeneigenwertprobleme") mit der Matlab-Function eig, die graphische Ausgabe der ersten drei Eigenschwingungsformen und die Ausgabe der ersten drei Eigenfrequenzen in das Command Window. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

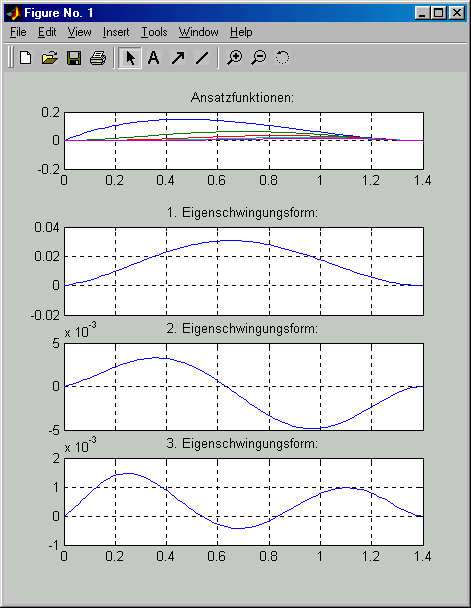 Die ersten beiden der in das Command Window ausgegebenen
Eigenfrequenzen zeigen eine ausgezeichnete Übereinstimmung mit den
Die ersten beiden der in das Command Window ausgegebenen
Eigenfrequenzen zeigen eine ausgezeichnete Übereinstimmung mit den