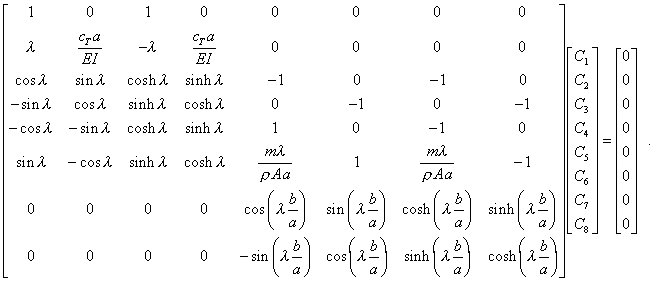|
|
||||||||||||||||||||||||
|
Im Skript “Biegeschwingungen gerader Träger” wird gezeigt, dass mit den oben eingezeichneten Koordinaten die Biegeverformung in der Form
mit
aufgeschrieben werden kann. Hierin enthält der Parameter
die gesuchte Eigenkreisfrequenz ω. Als Bezugslänge wurde (willkürlich) a gewählt. Die in der allgemeinen Lösung enthaltenen Konstanten C1 ... C8 müssen den folgenden 8 Rand- und Übergangsbedingungen genügen:
V
gilt. Mit der oben angegebenen Beziehung zwischen ω und λ wird daraus:
Wenn dies in die sechste Bedingung eingesetzt wird, kürzt sich die Zeitfunktion T heraus, und es verbleibt:
Mit dieser und den 7 anderen Rand- und Übergangsbedingungen kann nun das Gleichungssystem für die 8 Integrationskonstanten formuliert werden:
Das homogene Gleichungssystem hat nur dann nichttriviale Lösungen, wenn die Koeffizientendeterminate verschwindet. Aus dieser Bedingung können die (unendlich vielen) Werte für λ berechnet werden (Eigenwerte), aus denen sich dann die Eigenkreisfrequenzen bzw. Eigenfrequenzen berechnen lassen. Für diese Eigenwerte existieren nichttriviale Lösungen (nicht alle Ci sind gleich 0), die sich jedoch nur bis auf einen willkürlichen Faktor bestimmen lassen. Das nachfolgende MATLAB-Script realisiert diese Berechnungen mit folgender Strategie:
|
|
|
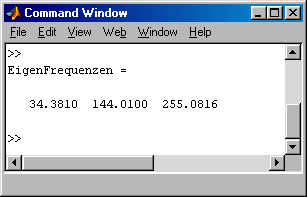
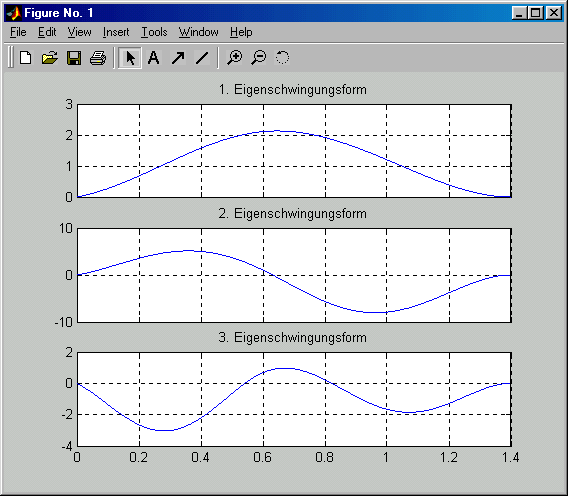
Mit dem Script werden die drei kleinsten Einfrequenzen berechnet und in das Command Window ausgegeben. Die zugehörigen Eigenschwingungsformen werden in ein separates Graphik-Fenster gezeichnet:
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

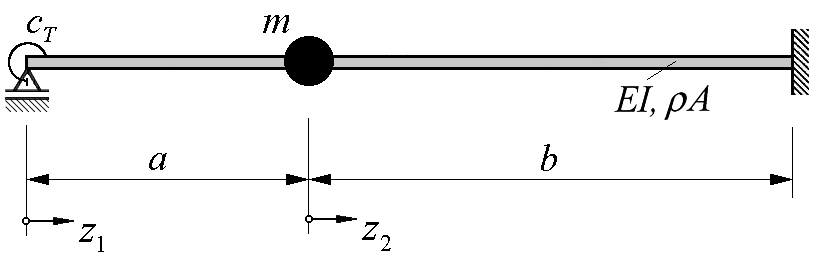
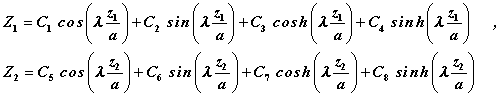
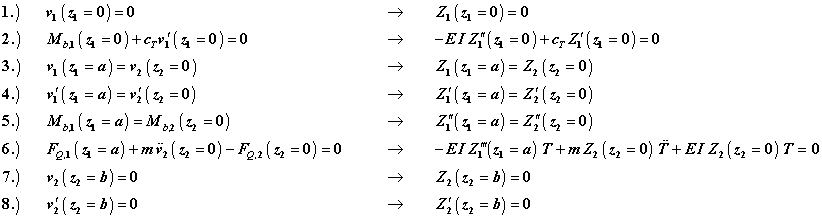
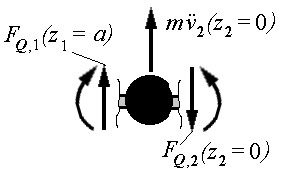 or der Aufstellung des Gleichungssystems für die Konstanten C1 ... C8 muss die sechste Bedingung (Kraftgleichgewicht an der Masse m,
nebenstehende Skizze) noch bearbeitet werden: Im Skript “
or der Aufstellung des Gleichungssystems für die Konstanten C1 ... C8 muss die sechste Bedingung (Kraftgleichgewicht an der Masse m,
nebenstehende Skizze) noch bearbeitet werden: Im Skript “