|
|
||||||||||||||||||||||||
|
Im Skript “Biegeschwingungen gerader Träger” wird gezeigt, dass eine beliebige Ansatzfunktion, die die geometrischen Randbedingungen erfüllt, in der Regel recht schlechte Näherungen liefert. Dagegen kann eine elastostatische Biegelinie mit einer “passenden” Belastung eine ausgezeichnete Näherung liefern.
(vgl. “Dankert/Dankert: Technische Mechanik”, Seiten 246 und 247) bietet sich dafür an, wobei nur der Inhalt der eckigen Klammer verwendet werden muss:
Der Rayleighsche Quotient (siehe Skript “Biegeschwingungen gerader Träger”) vereinfacht sich für diese Aufgabe zu
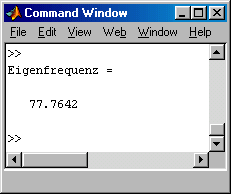
Der in das nachfolgend zu sehende Command Window ausgegebene Wert für die kleinste Eigenfrequenz ist eine ausgezeichnete Näherung des “exakten” Wertes f1,exakt = 77,60 s - 1 .
Biegesteifigkeit und Massebelegung werden in den Zeilen 17 und 18 als Vektoren mit Werten für alle Stützpunkte belegt, dies kann gegebenenfalls für andere Aufgaben beliebig modifiziert werden. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

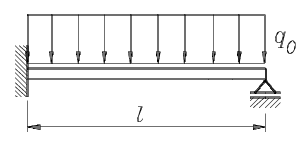 Die Biegelinie für den nebenstehend skizzierten Belastungsfall
Die Biegelinie für den nebenstehend skizzierten Belastungsfall
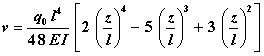
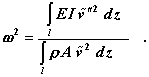
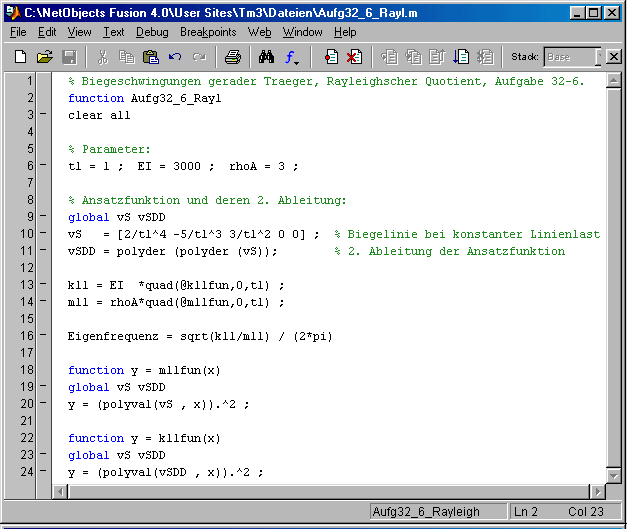 Das nebenstehend zu sehende Matlab-Script
zeigt die Lösung, wobei die bestimmten Integrale mit der Matlab-Function quad berechnet werden.
Das nebenstehend zu sehende Matlab-Script
zeigt die Lösung, wobei die bestimmten Integrale mit der Matlab-Function quad berechnet werden.
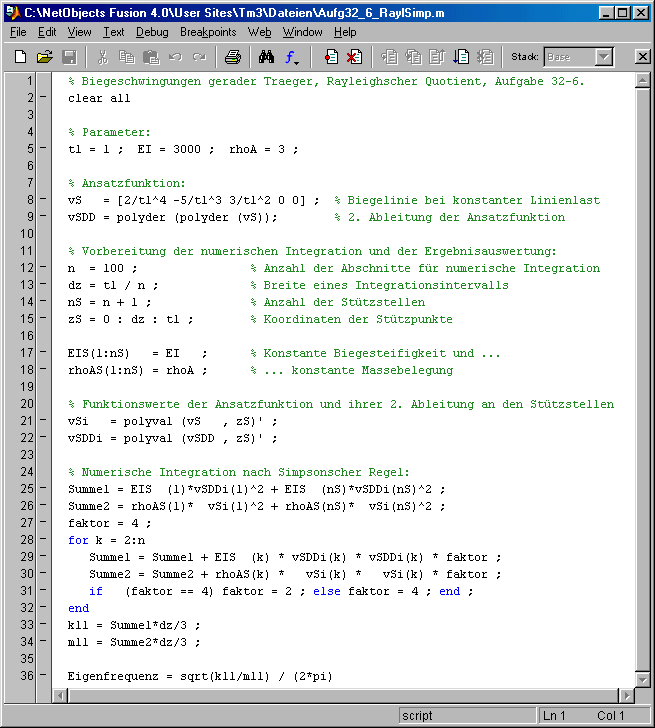 Wenn Biegesteifigkeit und/oder
Massebelegung nicht konstant sind (z. B. nur bereichsweise konstant), kann die Verwendung der Matlab-Function quad wegen der Notwendigkeit der Bereitstellung einer Function für die Berechnung des Integranden etwas
umständlich sein. Deshalb wird hier (nebenstehend) auch noch ein Matlab-Script für diese Aufgabe angegeben, das wie das
Wenn Biegesteifigkeit und/oder
Massebelegung nicht konstant sind (z. B. nur bereichsweise konstant), kann die Verwendung der Matlab-Function quad wegen der Notwendigkeit der Bereitstellung einer Function für die Berechnung des Integranden etwas
umständlich sein. Deshalb wird hier (nebenstehend) auch noch ein Matlab-Script für diese Aufgabe angegeben, das wie das 


