
|
|
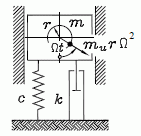
Eine Masse m ist linear-elastisch gelagert (Feder mit Federzahl c). Sie wird durch eine mit der Drehzahl n umlaufende Unwucht mu r zu Schwingungen angeregt, die geschwindigkeitsproportional gedämpft werden (Dämpfungskonstante k). Die Animation zeigt den stationären Schwingungszustand. |
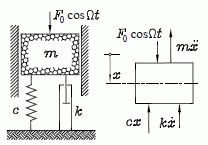
Theorie der unwuchterregten Schwingung
Eine Masse m ist linear-elastisch gelagert (Federzahl c) und wird von einer periodisch veränderlichen Kraft zu harmonischen Schwingungen angeregt. Bei einer geschwindigkeitsproportionalen Dämpfung (Dämpfungskonstante k) wird die Bewegung durch folgende Differenzialgleichung beschrieben (die Koordinate x hat ihren Ursprung in der statischen Ruhelage des Systems):
![]()
Die Differenzialgleichung wird unter Verwendung der in der Technischen Mechanik üblichen Symbole ω (Eigenkreisfrequenz der freien ungedämpften Schwingung) und D (so genanntes Lehrsches Dämpfungsmaß) entsprechend
![]()
umgeschrieben:
![]()
Es ist eine inhomogene lineare Differenzialgleichungen mit konstanten Koeffizienten. Ihre allgemeine Lösung kann als Summe der allgemeinen Lösung xhom der zugehörigen homogenen Differenzialgleichung und einer beliebigen Partikulärlösung xpart der inhomogenen Differenzialgleichung zusammengesetzt werden. Die Lösung wird ausführlich beschrieben im Bereich "Mathematik für die Technische Mechanik" auf der Seite "Beispiel: Erzwungene gedämpfte Schwingungen". Dort wird auch gezeigt, dass nach einem (in der Regel recht kurzen) Einschwingvorgang die Bewegung ausschließlich durch die Partikulärlösung der Differenzialgleichung beschrieben wird. Es ist die sogenannte
Stationäre Lösung: Nach einer bestimmten Einschwingzeit schwingt der durch die harmonisch veränderliche Kraft F0 cos Ωt erregte gedämpfte Schwinger nach dem Bewegungsgesetz:
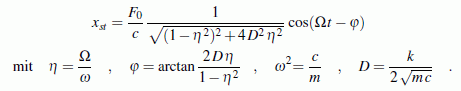
Die Schwingung im stationären Zustand erfolgt mit der Erregerkreisfrequenz Ω. Die Amplitude der stationären Schwingung ist konstant. Die Schwingung erfolgt in der Regel nicht "im gleichen Takt" mit der Erregung, was in der Lösung durch die so genannte "Phasenverschiebung" φ repräsentiert wird.
Die Größe der Amplitude (Ausdruck vor der cos-Funktion) wird wesentlich vom Abstimmungsverhältnis η (Quotient von Erregerkreisfrequenz Ω und Eigenkreisfrequenz ω des ungedämpften Schwingers) bestimmt.
Wenn die Erregerkraft durch eine mit der Winkelgeschwindigkeit Ω umlaufende Unwucht mur erzeugt wird, ist F0 die Fliehkraft (Produkt aus Unwuchtmasse mu, Radius r und dem Quadrat der Winkelgeschwindigkeit, Bild rechts oben auf dieser Seite):
![]()
und aus der oben angegebenen allgemeinen Lösung für den harmonisch erregten Schwinger wird die "Bewegung im stationären Zustand für den unwuchterregten Schwinger"
![]()
mit der "Vergrößerungsfunktion für die Unwuchterregung"
![]()
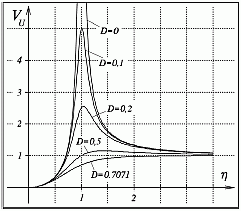
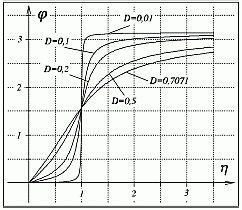
Die Amplitude ist die wichtigste Kenngröße der erzwungenen Schwingung, unabhängig davon, ob die die Schwingung erwünscht ist (z. B.: Schwingsieb) oder nicht (z. B.: Fundamentschwingungen von Arbeitsmaschinen). Bei unwuchterregten Schwingungen ist ihre Größe linear proportional zur Größe der Unwucht mur, hängt aber auch sehr stark vom Abstimmungsverhältnis und der Dämpfung ab. Das nachfolgende Diagramm links zeigt den Einfluss dieser beiden Parameter auf die Vergrößerungsfunktion, deren Wert die Größe der Amplitude in der Regel wesentlich stärker als die Größe der Unwucht beeinflusst. Rechts sieht man die Phasenverschiebung φ, die die zeitliche Verschiebung der Amplitude der Masse m zur Amplitude der Erregung zeigt:
|
|
|
| Vergrößerungsfunktion | Phasenverschiebung |
- Bei sehr kleiner Dämpfung nimmt die Vergrößerungsfunktion in der Nähe von η = 1 sehr große Werte an (für D = 0 hat sie bei η = 1 eine Polstelle). Eine Erregung mit einer Winkelgeschwindigkeit Ω, die der Eigenkreisfrequenz ω des ungedämpften Schwingers entspricht, führt bei kleiner Dämpfung zu sehr großen Amplituden (Resonanz).
- Im überkritischen Bereich (η > 1) nähern sich die Werte aller Vergrößerungsfunktionen VU dem Wert 1: Für hohe Erregerfrequenzen sind die Amplituden der unwuchterregten Schwingung von der Erregerfrequenz und der Dämpfung nahezu unabhängig.
- Für Dämpfungswerte D < 0,7071
haben die Kurven ein Maximum, das rechts von der Stelle
η = 1 bei
liegt. Die zugehörige Erregerkreisfrequenz ist weder mit der Eigenkreisfrequenz des gedämpften noch mit der des ungedämpften Schwingers identisch, ηmax liegt aber für kleine Dämpfungswerte sehr nahe bei 1 (Erregerkreisfrequenz gleich Eigenkreisfrequenz des ungedämpften Schwingers).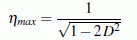
- Die Phasenverschiebung φ ist wie folgt zu interpretieren: Maxima, Minima und Nullstellen der Erregerkraft fallen mit den entsprechenden Punkten des Bewegungsgesetzes der Masse m zeitlich nicht zusammen. Bei sehr kleiner Dämpfung ist φ im unterkritischen Bereich annähernd Null, die Bewegung erfolgt phasengleich zur Erregung. Im überkritischen Bereich gilt bei kleiner Dämpfung φ ≈ π, und die Bewegungsrichtung des Schwingers ist stets der Richtung der Erregerkraft entgegengerichtet. Für η = 1 (Resonanzfall) gilt immer: φ = π/2.
Alle diese Phänomene kann man durch Variation der Parameter mit der interaktiven Animation oben auf dieser Seite veranschaulichen. Dazu werden nachfolgend einige Empfehlungen gegeben.
Empfehlungen zum "Spielen mit der Animation"
- Beim Start dieser Seite hat die Unwucht eine Drehzahl von n = 600 min−1, was einer Erregerfrequenz Ω = 62,8319 s−1 entspricht. Weil die Eigenkreisfrequenz des ungedämpften Schwingers (Masse: 50 kg, Federzahl 260000 N/m) mit ω = 72,111 s−1 größer ist (Abstimmungsverhältnis η = 0,871321), befindet sich der Schwinger im unterkritischen Bereich. Er schwingt mit der recht kleinen Amplitude xmax = 0,01619 mm. Deutlich zu erkennen ist die Phasenverschiebung: Wenn sich die (rote) Unwucht bereits wieder aufwärts (abwärts) bewegt, ist die Bewegung der Masse m immer noch abwärts (aufwärts) gerichtet.
- Ohne Dämpfung (k = 0 kg/s eintragen und auf "Werte übernehmen" klicken) vergrößert sich die Amplitude erheblich, so dass der Längenmaßstab der Animation geändert werden muss (geschieht automatisch). Die Phasenverschiebung der Schwingung verschwindet, die Bewegungen der roten Unwucht und der schwingenden Masse sind synchron.
- Bei einer Erhöhung der Drehzahl der Unwucht auf n = 700 min−1 vergrößert sich die Amplitude noch einmal erheblich, weil der Schwinger nun mit einem Abstimmungsverhältnis η = 1,01654 recht nah an der Resonanzstelle liegt. Weil es außerdem nun der überkritische Bereich ist, liegt die Phasenverschiebung bei φ = 180°: Während der kompletten Abwärtsbewegung der Unwucht bewegt sich die Masse aufwärts und umgekehrt.
- Der Versuch, das Programm mit der Resonanzfrequenz zum Crash zu bringen, misslingt (vermutlich), weil in der Grafik der Maßstab für die Amplitude stets angepasst wird und wegen der unvermeidlichen Rundungsfehler bei der internen Rechnung die exakte Übereinstimmung von Erregerfrequenz und Resonanzfrequenz kaum gelingen kann. Immerhin führt zum Beispiel eine Drehzahl n = 688,61 min−1 auf eine (theoretische) Amplitude von xmax = 16002 mm.
