|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Zur Startseite |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
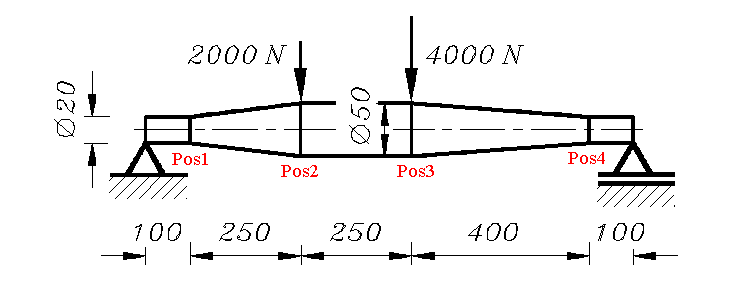
Die Ergebnisse für die Berechnung der Durchbiegung der stückweise konischen Welle (Elastizitätsmodul: E = 210000 N/mm2) nach der Finite-Elemente-Methode sollen mit dem RITZschen Verfahren verifiziert werden. Die nachfolgend gelistete m-Datei lässt die Berechnung mit maximal 5 Polynom-Ansätzen zu, die jeweils für die gesamte Welle gelten: v = a1 [- (z/l)2 + z/l] + a2 [-(z/l)3 + (z/l)2] + a3 [(z/l)4 - 2(z/l)3 + (z/l)2]
Jede Funktion erfüllt für sich die geometrischen Randbedingungen (l ist die Gesamtlänge der Welle), die beiden letzten Funktionen auch die Bedingung der Momentenfreiheit an den Rändern. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
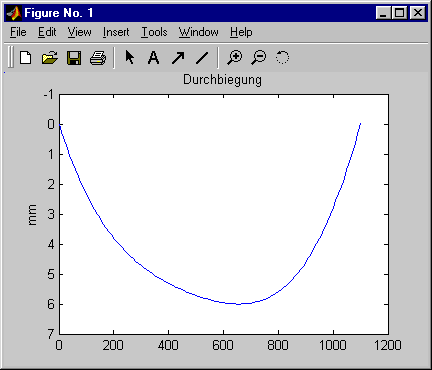
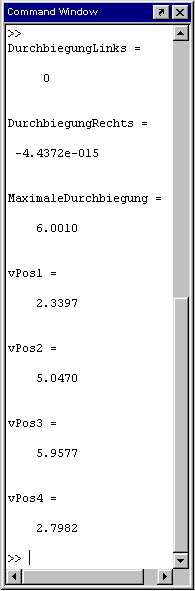
Die am Ende der Datei farblich hervorgehobenen Zeilen sorgen für die graphische Ausgabe der Biegelinie (Bild unten) und die Ausgabe der Durchbiegung an den markanten Punkten (in das “Command Window”, Bild rechts), dies sind jeweils die Stellen des Übergangs vom konstanten Querschnitt auf einen veränderlichen Querschnitt bzw. umgekehrt.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Die Ergebnisse zeigen, dass die Qualität sich trotz der 5 Ansatzfunktionen in Grenzen hält, als Verifikation der mit der FEM berechneten Ergebnisse sind sie allerdings durchaus brauchbar. Die oben angegebene m-Datei kann durch Modifikation der am Anfang farblich gekennzeichneten Zeile (m = 5) die Berechnung mit weniger Ansatzfunktionen ausführen. Die nachfolgende Tabelle zeigt, dass sich (wie zu erwarten) die Ergebnisse, die von “unbrauchbar” (eine oder zwei Ansatzfunktionen) bis zu “Abweichungen um etwa 10%” (fünf Ansatzfunktionen) reichen, mit zunehmender Anzahl der Ansatzfunktionen verbessert: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||