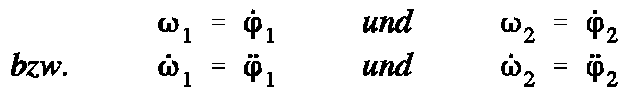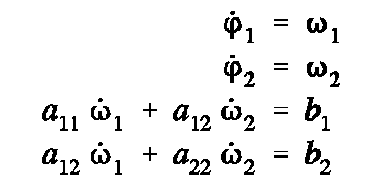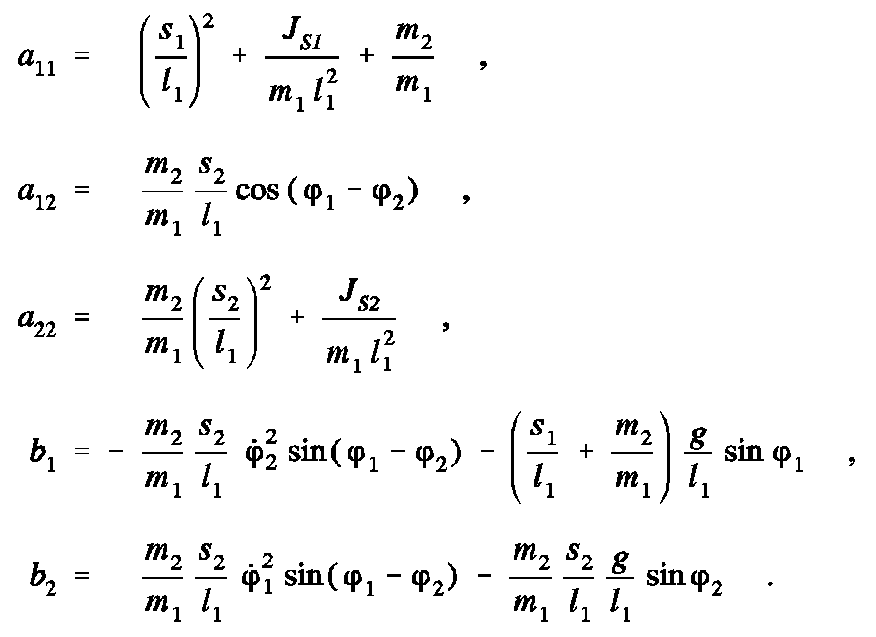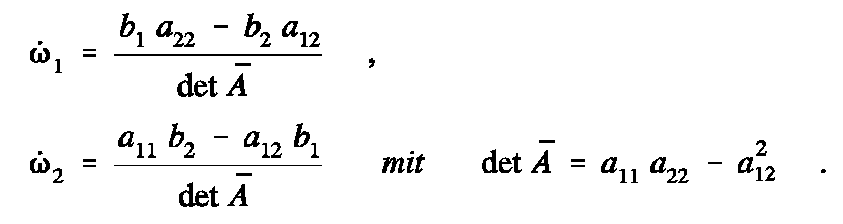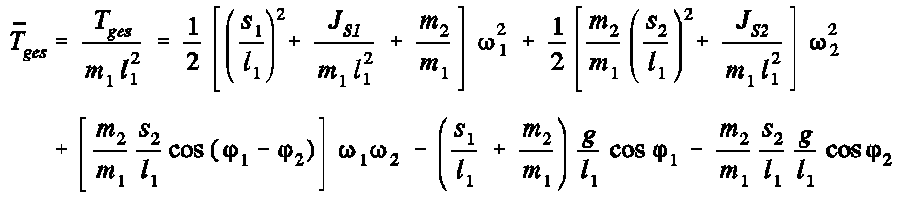|
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
Zur Startseite
|
|
|
|
 |
|
|
|
|
 |
|
|
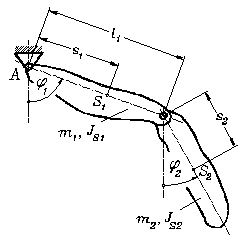
Doppelpendel, Lösung mit CAMMPUS
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
Die Bewegung eines Doppelpendels wird mit einem nichtlinearen Diffenzialgleichungssystem 2. Ordnung beschrieben. Die Differenzialgleichungen sind in den Beschleunigungsgliedern gekoppelt.
Mit dem CAMMPUS-Programm “Taschenrechner” können Differenzialgleichungssysteme 1. Ordnung gelöst werden. Deshalb wird durch Einführen der neuen Variablen
|
|
|
|
|
|
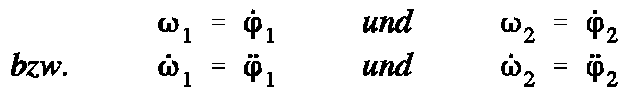 |
|
|
|
aus den beiden Differenzialgleichungen 2. Ordnung ein System von 4 Differenzialgleichungen 1. Ordnung, von denen zwei in den Ableitungen gekoppelt sind. Das Differenzialgleichungssystem kann z. B.
so formuliert werden:
mit
Die ai j und bi werden als Funktionen definiert, so dass die beiden in den Ableitungen
gekoppelten Differenzialgleichungen entkoppelt werden können, wenn man das Gleichungssystem, das sie darstellen, z. B. nach der Cramerschen Regel auflöst:
Damit ist ein Satz von Funktionen gegeben, der dem Programm MCALCU angeboten werden kann. |
|
|
|
|
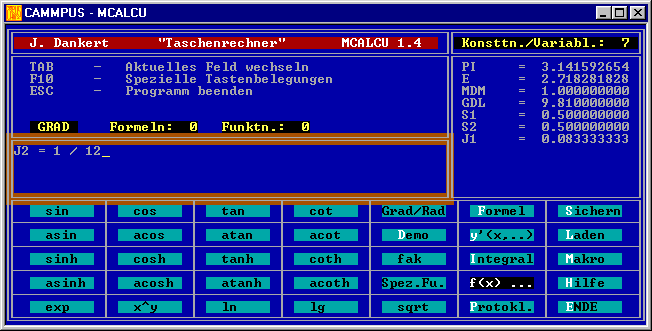
CAMMPUS starten und “Taschenrechner” wählen. Im Startmenü werden zunächst die Problemparameter als Konstanten definiert. Der nachfolgende Bildschirm-Schnappschuss zeigt den Startbildschirm des “Taschenrechners” mit dem bereits im Konsttn./Variabln.-Speicher zu sehenden Werten unmittelbar vor dem Betätigen der Eingabetaste für die Definition der letzten der 6 Konstanten:
|
|
|
|
|
 |
|
|
|
|
Man beachte: Bei der Eingabe von Funktionen und Differenzialgleichungen wird stets die syntaktische Richtigkeit überprüft, insbesondere wird darauf geachtet, dass nur
Konstanten, Variablen und Funktionen benutzt werden, die bereits vorher definiert wurden.
|
|
|
|
|
Deshalb müssen in diesem Fall (nach der Definition der Konstanten S1, S2, MDM, . . . ) die Funktionen A11, A12, . . . , DET vor den Differenzialgleichungen, die diese
Funktionen enthalten, definiert werden. Der dabei entstehende Konflikt, dass die Funktionen die Variablen PHI1, PHI2, OMEG1 und OMEG2 enthalten, die normalerweise erst im Zusammenhang mit den Differenzialgleichungen
(durch Zuweisen ihrer Anfangswerte) definiert werden, kann auf zwei verschiedene Arten gelöst werden:
- Vor der Definition der Funktionen werden die Variablen PHI1, PHI2, OMEG1 und OMEG2 (zweckmäßigerweise gleich mit ihren Anfangswerten) als Konstanten
definiert, dann können die Funktionen (vor den Differenzialgleichungen) über "f(x) ..." und "Definieren" eingegeben werden.
- Man kann jedoch auch mit dem Menüangebot "y'(x,..)" beginnen. In diesem Fall werden zunächst die Anfangswerte abgefragt (und PHI1, PHI2, OMEG1 und
OMEG2 werden dabei automatisch definiert). Dann muss man jedoch bei der Abfrage der Differenzialgleichungen über die Funktionstaste F6 ("Funktion vor Differentialgleichung definieren") das
"Sonderangebot" ansteuern, mit dem Funktionsdefinitionen einzugeben sind, bevor die Differenzialgleichungen definiert werden.
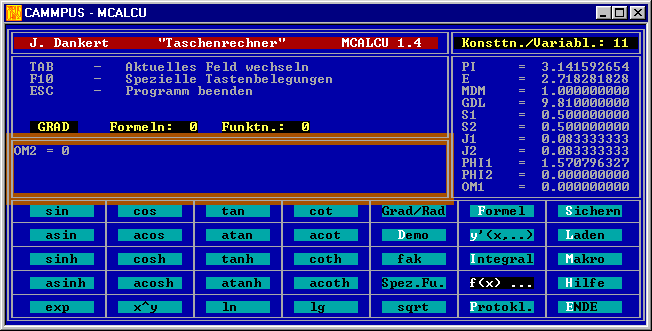
Nachfolgend werden Bildschirm-Schnappschüsse gezeigt, die der erstgenannten Variante entsprechen (ohne dass damit eine Präferenz für diesen Weg ausgesprochen wird). Der folgende
Bildschirm zeigt die Situation, nachdem drei Variablen mit ihren Anfangswerten bereits als Konstanten definiert wurden, unmittelbar vor der Eingabe der letzten Variablen:
|
|
|
|
|
 |
|
|
|
|
Nun können über f(x)... und Definieren die Funktionen definiert werden.
Die Reihenfolge (nur jede Funktion greift auf vorher definierte Funktionen zurück) könnte wie in dem nebenstehenden Listing der Datei gewählt werden, die man über das
Menüangebot Sichern nach der Eingabe der Funktion erzeugen kann.
Als erste Aktion sollte die Funktionsvariable auf T umgestellt werden. Es können auf diesem Wege auch gleich die Differentilagleichungen mit definiert werden: Eine Funktion,
deren Name mit dem Zeichen ‘ endet, wird automatisch als Differenzialgleichung interpretiert.
|
|
|
|
|
|
!! "Taschenrechner" MCALCU: Funktionen !!
!
! Funktionsvariable:
T
!
A11 = S1^2+J1+MDM
~~~
A12 = MDM*S2*COS(PHI1-PHI2)
~~~
A22 = MDM*S2^2+J2
~~~
B1 = -MDM*S2*OM2^2*SIN(PHI1-PHI2)-(S1+MDM)*GDL*SIN(PHI1)
~~~
B2 = MDM*S2*OM1^2*SIN(PHI1-PHI2)-MDM*S2*GDL*SIN(PHI2)
~~~
DET = A11*A22-A12^2
~~~
PHI1' = OM1
~~~
OM1' = (B1*A22-B2*A12)/DET
~~~
PHI2' = OM2
~~~
OM2' = (A11*B2-A12*B1)/DET
~~~
|
|
|
|
|
|
|
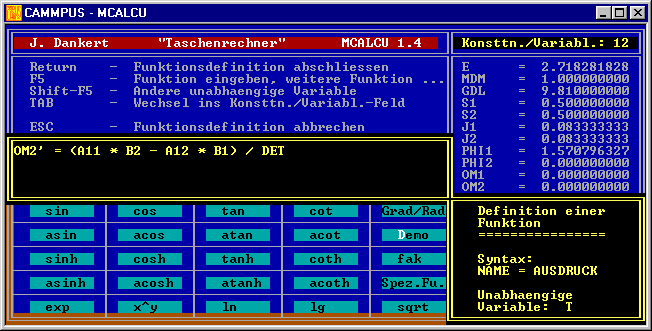
Der folgende Bildschirm-Schnappschuss zeigt die Definition der letzten Funktion (Differentialgleichung OM2’ = ...):
|
|
|
|
|
 |
|
|
|
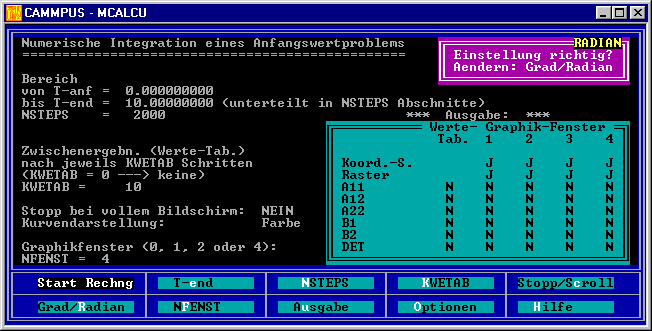
Nach Eingabe der Funktionen und der Differenzialgleichugen wird y’(x,..) und Loesen gewählt. Es erscheint folgende Maske:
|
|
|
|
|
 |
|
|
|
Testrechnungen ergaben, dass eine stabile Rechnung über das voreingestellte Zeitintervall von 10 Sekunden erst mit 2000 Integrationsschritten erreicht werden kann. Deshalb
ist diese Änderung in der Eingabemaske bereits vorgenommen worden. Auf jeden Fall muss die Interpretation der Argumente der Winkelfunktionen auf RADIAN umgestellt werden. Alle anderen Voreinstellungen können
akzeptiert werden. Es wird danach “Start Rechnung” gewählt.
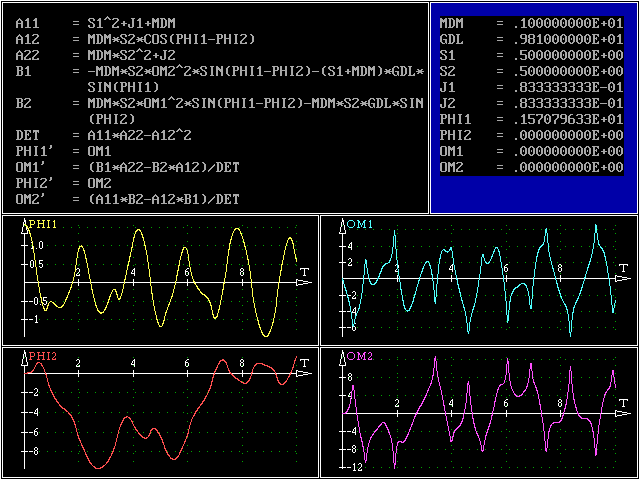
Wertetabellen der berechneten Funktionswerte und deren graphische Darstellung werden automatisch erzeugt. Von den verschiedenen Möglichkeiten der Darstellung der Ergebnisse
ist nachfolgend die über das “Graphik+”-Angebot erreichbare Ausgabe der definierten Funktionen (einschließlich der Differenzialgleichungen), der Konstanten und der graphischen Darstellung der vier Funktionsverläufe
zu sehen:
|
|
|
|
|
 |
|
|
|
|
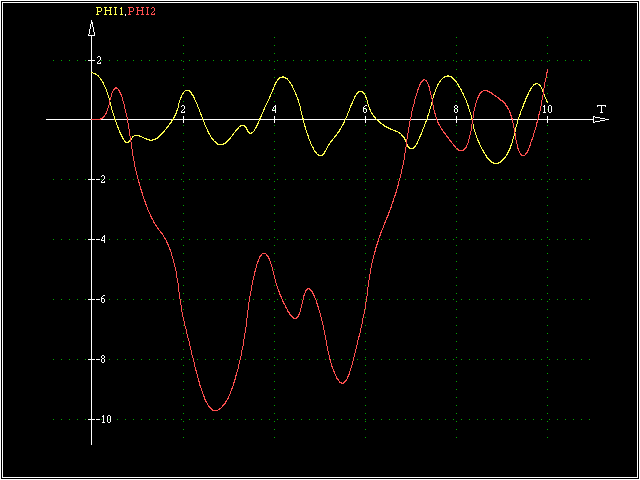
Die recht bizarren Funktionsverläufe spiegeln den tatsächlich außerordentlich komplizierten Bewegungsablauf eines solchen Doppelpendels wider. Während das obere Pendel eine
recht unregelmäßige Schwingung ausführt, beginnt das untere Pendel mit einem "Salto", dem bald darauf ein "Salto rückwärts" folgt (nebenstehend sind φ1 (t) und
φ2 (t) gemeinsam in einem GraphikFenster dargestellt).
Der komplizierte Formelsatz, der mit dem programminternen mathematischen Parser bei 2000 Runge-Kutta-Schritten 8000 Mal ausgewertet werden muss, schlägt sich natürlich in einer
Rechenzeit im Sekundenbereich nieder.
|
|
|
 |
|
|
|
|
|
|
Andererseits ist diese theoretische Bewegungssimulation der praktischen Simulation überlegen. Nach etwa 4 bis 5 Sekunden weicht auch bei sehr genauer Versuchsdurchführung die berechnete
Bewegung von der des Modells ab, was nicht an der Berechnung, auch nicht an den Idealisierungen (Reibungsfreiheit, Vernachlässigung von Bewegungswiderständen) liegt. Die Anfangsbedingungen sind jedoch praktisch nie
so genau zu realisieren, dass bei Versuchswiederholungen gleichbleibende Resultate über ein längeres Zeitintervall zu erzielen sind. Wenn Theorie und Praxis nicht übereinstimmen, ist das (wie hier) manchmal peinlich
für die Praxis.
|
|
|
|
|
|
Zur Schrittweitenwahl bei der numerischen Integration von Differenzialgleichungen:
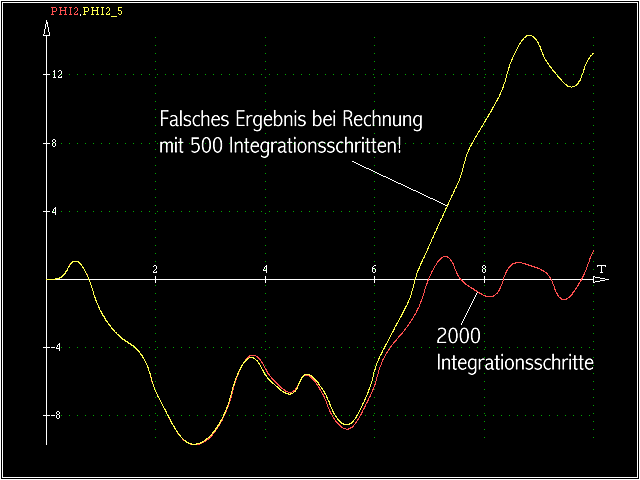
Das Doppelpendel-Beispiel mit seinen bizarren Bewegungsgesetzen sollte Anlass sein, mit der Schrittweite zu experimentieren, denn mit der Voreinstellung in vielen Programmen
(bei CAMMPUS: 500 Schritte für das zu berechnende Intervall) werden bei diesem Problem falsche Ergenisse abgeliefert:
|
|
|
|
 |
|
|
|
Die nebenstehenden Kurven zeigen, dass über ein bestimmtes Intervall durchaus auch mit der groben Schrittweite brauchbare Ergebnisse entstehen. Ein langsames “Abdriften” von
den exakten Werten kann dann allerdings zu völlig falschen Bewegungs-Diagrammen führen.
Wenn man durch zwei Rechnungen mit unterschiedlichen Schrittweiten zu dieser Erkenntnis gekommen ist, muss man natürlich noch eine weitere Rechnung mit nochmals verfeinerter
Schrittweite starten.
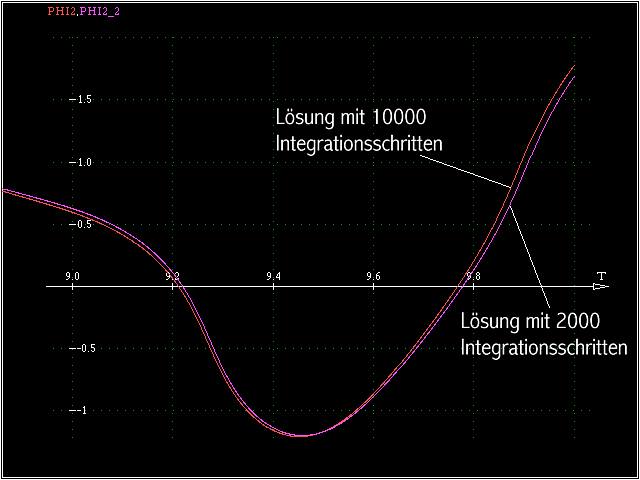
Eine Rechnung mit 10000 Integrationsschritten zeigt tatsächlich Kurvenverläufe, die mit denen der “2000er” Rechnung übereinstimmen, allerdings lässt ein sehr starker Zoom am
Ende des Intervalls (nebenstehendes Bild) noch geringfügige Abweichungen erkennen, die aber für die “10000er” Rechnung als sicher “ausreichend genau” sprechen (tatsächlich bestätigt eine “20000er” Rechnung alle
Funktionswerte auf mindestens 5 Stellen).
|
|
|
|
|
 |
|
|
|
|
|
|
Kontrolle durch Energiebetrachtung:
Wenn - wie in diesem Beispiel möglich - eine Kontrollfunktion zusätzlich berechnet werden kann, dann sollte man diese Möglichkeit unbedingt nutzen. Auf Seite 695 wird
empfohlen, die Gesamtenergie, die bei diesem System konstant sein muss, für jeden Integrationsschritt zusätzlich zu berechnen:
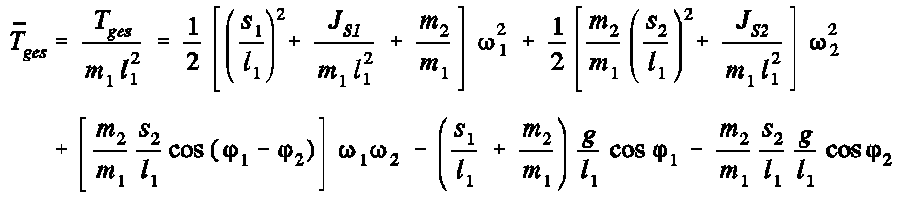
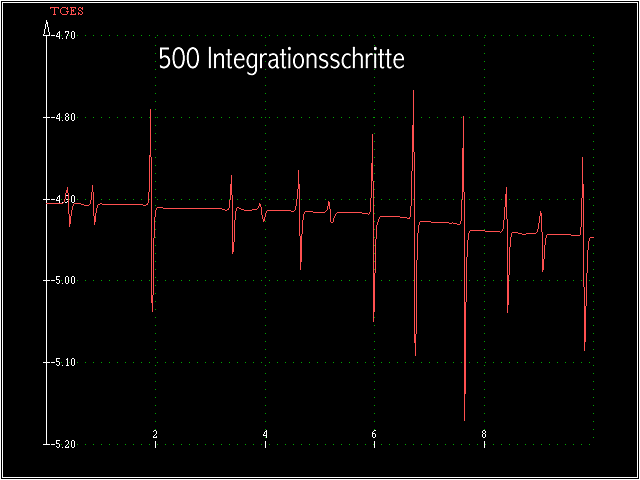
Die nachfolgenden Bildschirm-Schnappschüsse zeigen die “dimensionslose Gesamtenergie”:
|
|
|
|
 |
|
|
|
Die starken “Zacken” an den kritischen Stellen der Bewegung sind ein Indiz für die zu grobe Schrittweite, noch wesentlich bedenklicher ist der Abfall der Kurve, die
theoretisch einen konstanten Verlauf haben müsste. Die Kurve der Gesamtenergie zeigt sehr deutlich, dass 500 Integrationsschritte zu wenig sind.
|
|
|
|
|
|
 |
|
|
|
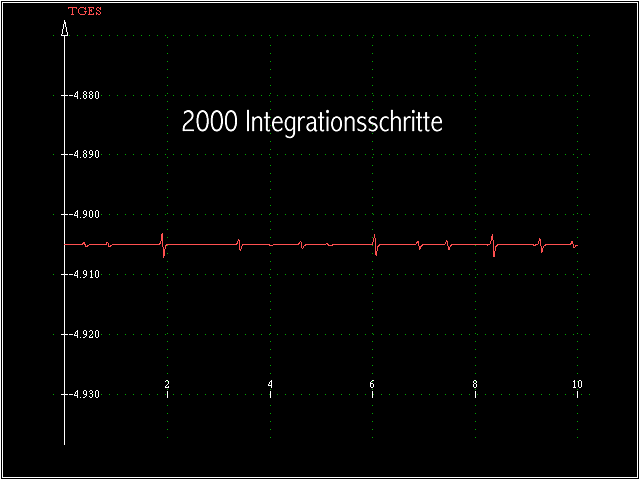
Bei 2000 Integrationsschritten ist der Kurvenverlauf “konstant”, allerdings zeigt ein sehr starker Zoom noch einige “Zacken”, ...
|
|
|
|
|
 |
|
|
|
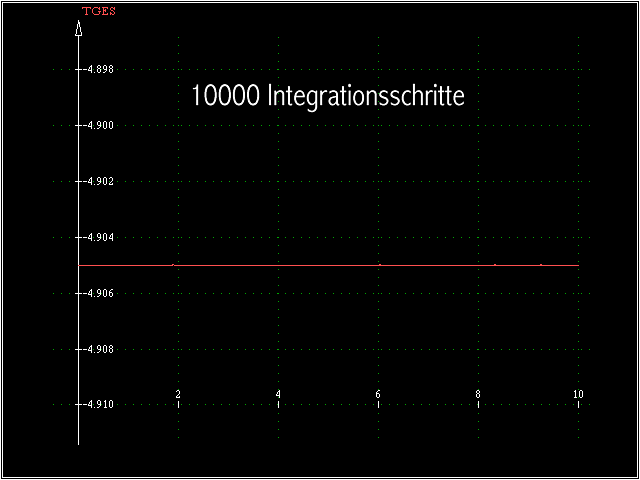
... die bei 10000 Integrationsschritten trotz eines noch deutlich stärkeren Zooms nicht mehr zu erkennen sind. Der zu erwartende konstante Wert für die “dimensionslose
Gesamtenergie” (4.905) zeigt sich für das gesamte Intervall: Die Rechnung ist “gesund”.
|
|
|
|
|
|
|
Dateien für dieses Beispiel, die zum Download verfügbar sind:
- Konstanten des Berechnungsmodells als Dopendel.con
,
- Funktionen (Differenzialgleichungen und die Funktion für die Gesamtenergie) als Dopendel.fcn
.
|
|
|
|
Homepage TM-aktuell
|
|
|
|
www.JürgenDankert.de
|
|
|
 |
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
D
|
 |
|
nkert.de
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|