Aufgabe
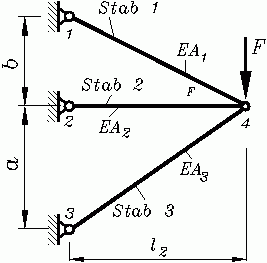
Das skizzierte System ist durch eine Kraft F belastet. Der Stab 2 soll um die Temperaturdifferenz ΔT erwärmt werden. Die Verschiebungen des Kraftangriffspunktes und die Stabkräfte sind zu berechnen.
Gegeben:
EA1 = 5·106 N ;
a = 320 mm ;
αt = 1,2·10−5 K−1 ;
EA2 = 8·106 N ;
b = 240 mm ;
ΔT = 200 K ;
EA3 = 2·106 N ;
l2 = 450 mm ;
F = 3000 N .
Physikalisches Modell des Problems
| Knoten-Informationen | ||||||
| Kn.-Koord. | Kn.-Lasten | u-verh. | ||||
| Kn. | x | y | Fx | Fy | ux | uy |
| 1 | 0 | 240 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 0 | 0 | 1 | 1 |
| 3 | 0 | -320 | 0 | 0 | 1 | 1 |
| 4 | 450 | 0 | 0 | -3000 | 0 | 0 |
| Element-Informationen | ||||
| Topologie | Parameter | |||
| El. | Kn. | Kn. | EA | αt Δt |
| 1 | 1 | 4 | 5·106 | 0 |
| 2 | 2 | 4 | 8·106 | 240·10-5 |
| 3 | 3 | 4 | 2·106 | 0 |
Das physikalische Modell muss mit 3 "Knoten-Informationen" beschrieben werden: Knoten-Koordinaten, hier bezogen auf ein Koordinatensystem mit Ursprung im mittleren Lager, Knoten-Lasten und die Information, welche Knotenverschiebungen verhindert sind. Zusätzlich werden 2 "Element-Informationen" benötigt: Topologie (an welchen Knoten ist ein Element angeschlossen) und Element-Parameter (hier: Dehnsteifigkeit EA und Temperaturbelastung αt ΔT. Die Tabelle links zeigt die Knoten-Informationen, rechts sieht man die Element-Informationen, alles geordnet in 5 Matrizen, die das physikalische Modell komplett beschreiben.
Rechnung mit Matlab-Femset
Im "Finite-Elemente-Baukasten" Matlab-Femset ist das Stab-Element mit Temperaturbelastung vordefiniert. Man braucht also nur das physikalische Modell mit den 5 Matrizen (siehe oben) zu definieren und an den Modul "FEM-Algorithmus" femalg_m zu übergeben, der die Verschiebungen berechnet und abliefert. Im folgenden Matlab-Script findet man die oben definierten Matrizen wieder. Nur der farblich abgehobene Teil muss dem aktuellen Problem angepasst werden (das sind genau die Matrizen, die das Modell definieren:
clear all
xy = [0 240 ; 0 0 ; 0 -320 ; 450 0 ] ; % Kn.-Koord.
FK = [0 0 ; 0 0 ; 0 0 ; 0 -3000] ; % Kn.-Lasten
Lg = [1 1 ; 1 1 ; 1 1 ; 0 0 ] ; % u-verhindert
%
KM = [ 1 4 ; 2 4 ; 3 4] ;
EP = [5e6 0 ; 8e6 240e-5 ; 2e6 0] ;
% Finite-Elemente-Algorithmus:
[succ uv] = femalg_m (xy , KM , EP , Lg , FK)
if succ == 1 % Nach erfolgreicher Rechnung:
drawfw2duv (xy , KM , Lg , FK , uv) ; % Verformtes System zeichnen
sk = Stabkraefte2D (xy , KM , EP , uv) ; % Berechnung der Stabkraefte ...
for i = 1:3
disp (['Stab ',num2str(i), ': Stabkraft F = ',num2str(sk(i)),' N']) ;
end
figure ; % ... und zeichnen des Systems ..
drawfw2dsk (xy , KM , Lg , FK , sk , 'e') ; % ... in ein neues Graphik-Fenster
end
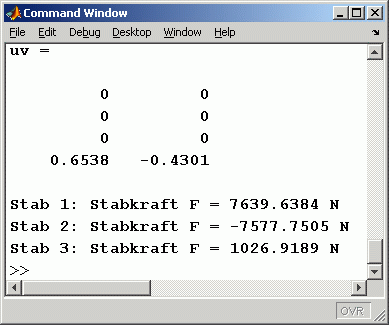
Der Modul femalg_m berechnet die Knotenverschiebungen und liefert sie im Command Window ab (nebenstehendes Bild). Man erkennt die Nullverschiebungen der drei gelagerten Knoten und die Horizontal- und Vertikalverschiebung des Kraftangriffspunktes.
Im Matlab-Script werden zusätzlich noch die Stabkräfte berechnet und ausgegeben, außerdem werden das verformte System und die Stäbe mit der farblichen Unterscheidung in Druck- und Zugstäbe in gesonderte Graphik-Fenster ausgegeben:
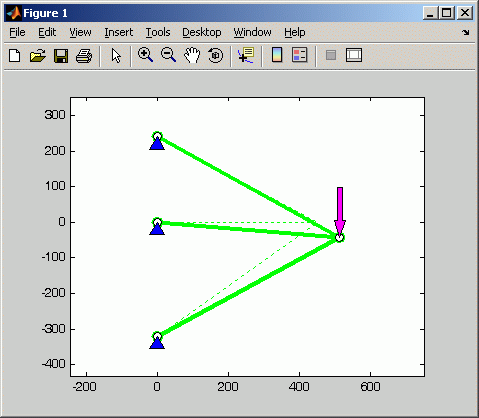
|
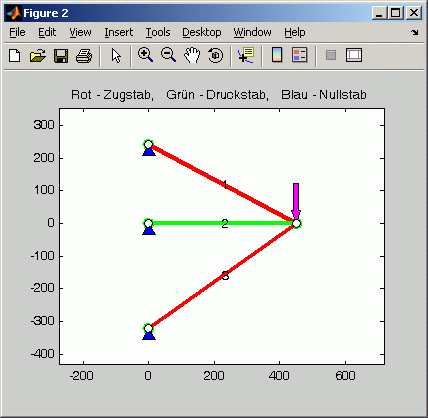
|
Das oben gelistete Matlab-Script und alle verwendeten Functions und DLLs stehen zum Download zur Verfügung: Stabdreischlag.m, Stabkraefte2D.m, drawfw2duv.m, drawfw2dsk.m, drawfw2d.m, elemat_m.dll, femalg_m.dll.
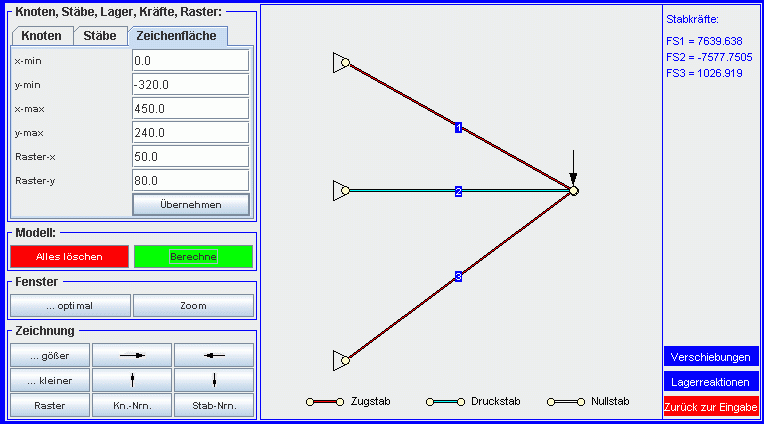
Interaktive Berechnung (www.TM-interaktiv.de)
Etwas einfacher ist natürlich die Nutzung des Programms "Statisch unbestimmte ebene Fachwerke", das unter www.TM-interaktiv.de angeboten wird. Man beachte allerdings, das das bequem mit ein paar Mausklicks zu erzeugende Modell genau die oben beschriebenen Informationen des physikalischen Modells enthält. Nach Eingabe des Modells ...
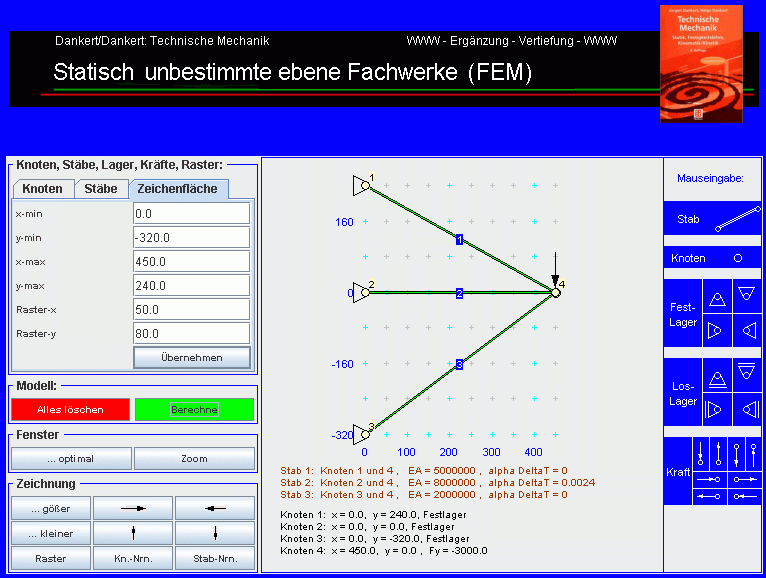
... und Anklicken des Button "Berechne" sieht man das verformte System, ...
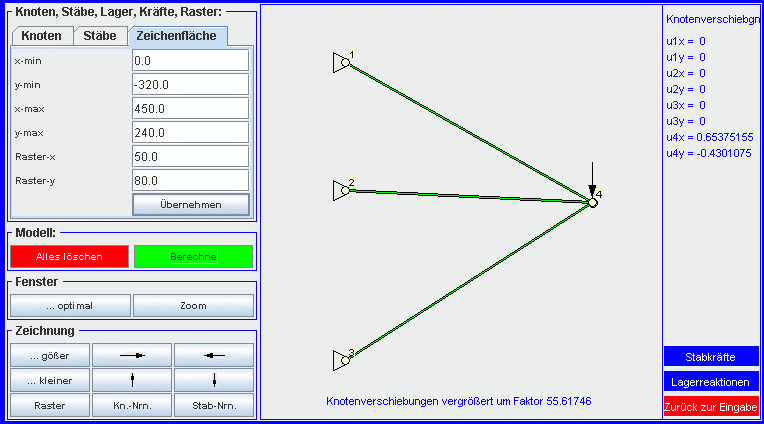
... und kann sich weitere Ergebnisse anzeigen lassen, zum Beispiel die Stabkräfte: