
Aufgabe
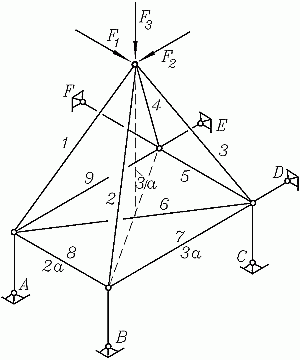
Für das skizzierte Fachwerk sind die Stabkräfte in den Stäben 1 bis 9 zu berechnen.
Gegeben: F1 = F2 = F3 = F.
Die Geometrie des Systems
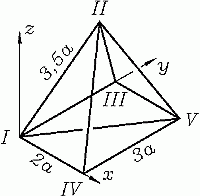
Die Geometrie des Fachwerks wird durch die Lage der 5 Knoten bestimmt, die entsprechend nebenstehender Skizze von I bis V nummeriert werden und in dem (willkürlich festgelegten) Koordinatensystem folgende Koordinaten haben:
| I | II | III | IV | V | |
| x | 0 | a | 0 | 2a | 2a |
| y | 0 | 1,5a | 3a | 0 | 3a |
| z | 0 | 3a | 0 | 0 | 0 |
Im Kapitel "Räumliche Probleme" wird gezeigt, dass die Stabkraft FS in einem Stab mit den Knoten i und j vektoriell folgendermaßen aufgeschrieben werden kann:
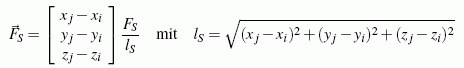
(lS ist die Länge des Stabs). In der angegebenen Form hat der Vektor die Richtung der Stabkraft am Knoten i.
Gleichgewichtsbedingungen
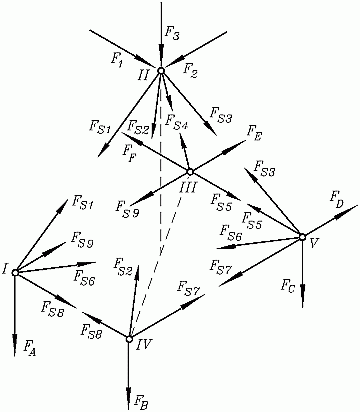
Rundumschnitte um die 5 Knoten machen die 15 Stabkräfte sichtbar (nebenstehende Skizze). An jedem Knoten können 3 Gleichgewichtsbedingungen formuliert werden, so dass 15 Gleichungen für die 15 Unbekannten zur Verfügung stehen.
Für das Aufschreiben der Gleichgewichtsbedingungen werden die Komponenten aller Kräfte in Richtung der gewählten Koordinaten benötigt. Die drei äußeren Kräfte F1, F2 und F3 und die Stabkräfte in den Stäben 5, 7, 8 und 9 wirken in Richtung einer der definierten Koordinatenachsen und müssen nicht in Komponenten zerlegt werden. Für die anderen Stäbe werden die Stabkräfte als Vektoren entsprechend der oben angegebenen Formel aufgeschrieben, aus denen die Komponenten dann abgelesen werden können.
Am Knoten I zum Beispiel wird der Vektor der Stabkraft im Stab 6 mit den Koordinaten des Knotens V als Punkt j und den Koordinaten des Knotens I als Punkt i aufgeschrieben. Der Vektor der Stabkraft im Stab 1 wird mit den Koordinaten des Knotens II als Punkt j und den Koordinaten des Knotens I als Punkt i aufgeschrieben. Mit den direkt aufzuschreibenden Vektoren der Stabkräfte der Stäbe 8 und 9 und des Lagerstabs A lauten also die Vektoren der 5 Stabkräfte am Knoten I:
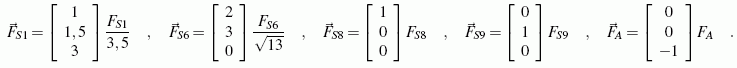
Nun können die drei Gleichgewichtsbedingungen für den Knoten I aufgeschrieben werden:
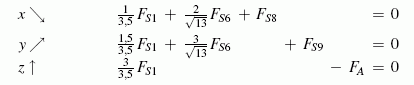
Auf gleichem Wege kommt man zu den Gleichgewichtsbedingungen der übrigen Knoten. Für den Knoten II ergibt sich:
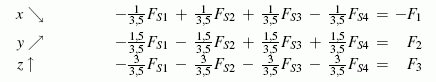
Die restlichen Gleichgewichtsbedingungen sind etwas einfacher:
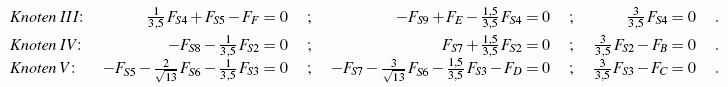
Lösung des Gleichungssystems mit Matlab
Das nachfolgend gelistete Matlab-Script (als Fachwerk3D_2.m zum Download verfügbar) baut das Gleichungssystem aus den 15 Gleichgewichtsbedingungen auf und löst es:
clear all
% 1 2 3 4 5 6 7 8 9 A B C D E F
A= [ 1/3.5, 0 , 0 , 0 , 0, 2/sqrt(13), 0, 1, 0, 0, 0, 0, 0,0, 0; %Ix
1.5/3.5, 0 , 0 , 0 , 0, 3/sqrt(13), 0, 0, 1, 0, 0, 0, 0,0, 0; %Iy
3/3.5, 0 , 0 , 0 , 0, 0 , 0, 0, 0,-1, 0, 0, 0,0, 0; %Iz
-1/3.5, 1/3.5, 1/3.5, -1/3.5, 0, 0 , 0, 0, 0, 0, 0, 0, 0,0, 0; %IIx
-1.5/3.5,-1.5/3.5, 1.5/3.5, 1.5/3.5, 0, 0 , 0, 0, 0, 0, 0, 0, 0,0, 0; %IIy
-3/3.5, -3/3.5, -3/3.5, -3/3.5, 0, 0 , 0, 0, 0, 0, 0, 0, 0,0, 0; %IIz
0 , 0 , 0 , 1/3.5, 1, 0 , 0, 0, 0, 0, 0, 0, 0,0,-1; %IIIx
0 , 0 , 0 ,-1.5/3.5, 0, 0 , 0, 0,-1, 0, 0, 0, 0,1, 0; %IIIy
0 , 0 , 0 , 3/3.5, 0, 0 , 0, 0, 0, 0, 0, 0, 0,0, 0; %IIIz
0 , -1/3.5, 0 , 0 , 0, 0 , 0,-1, 0, 0, 0, 0, 0,0, 0; %IVx
0 , 1.5/3.5, 0 , 0 , 0, 0 , 1, 0, 0, 0, 0, 0, 0,0, 0; %IVy
0 , 3/3.5, 0 , 0 , 0, 0 , 0, 0, 0, 0,-1, 0, 0,0, 0; %IVz
0 , 0 , -1/3.5, 0 ,-1,-2/sqrt(13), 0, 0, 0, 0, 0, 0, 0,0, 0; %Vx
0 , 0 ,-1.5/3.5, 0 , 0,-3/sqrt(13),-1, 0, 0, 0, 0, 0, 1,0, 0; %Vy
0 , 0 , 3/3.5, 0 , 0, 0 , 0, 0, 0, 0, 0,-1, 0,0, 0] ; %Vz
b = [ 0 ; 0 ; 0 ; -1 ; 1 ; 1 ; 0 ; 0 ; 0 ; 0 ; 0 ; 0 ; 0 ; 0 ; 0 ] ;
% Reihenfolge der Unbekannten im Ergebnisvektor x:
% FS1, FS2, ... FS9, FA, FB, FC, FD, FE, FF.
x = A\b

Nebenstehend sieht man das Ergebnis der Rechnung mit Matlab. Die letzten 6 Werte sind die Stabkräfte der Lagerstäbe A bis F. Diese Ergebnisse können verglichen werden mit einer Berechnung aus dem Kapitel "Räumliche Probleme", bei der sie auf ganz anderem Wege (6 Gleichgewichtsbedingungen am Gesamtsystem) gewonnen wurden.
