Aufgabe

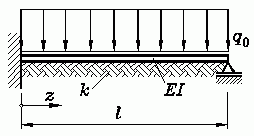
Für den skizzierten elastisch gebetteten Träger sind der Verlauf der Biegelinie und der Biegemomentenverlauf zu bestimmen.

Gegeben:

Lösung

Im Kapitel "Spezielle Biegeprobleme" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird gezeigt, dass die allgemeine Lösung der Differenzialgleichung der Biegelinie des elastisch gebetteten Trägers für die Durchbiegung v(z) die folgende Funktion liefert (v zählt positiv nach unten):

Die allgemeine Lösung muss für das behandelte Problem folgenden Randbedingungen angepasst werden:

1.) v(0) = 0 ;   2.) v'(0) = 0 ;   3.) v(l) = 0 ;   4.) v''(l) = 0 .

Diese Bedingungen ergeben ein lineares Gleichungssystem:

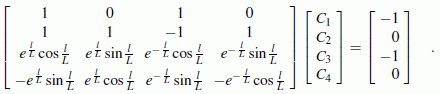
Der in den Gleichungen mehrfach vorkommende Quotient l/L berechnet sich mit den gegebenen Werten zu:

Nach Lösung des Gleichungssystems sind die Integrationskonstanten C₁ bis C₄ und damit die Biegelinie v(z) bekannt. Der Biegemomentenverlauf ergibt sich dann aus M_b(z) = −EIv''(z).