|
|
||||||||||||||||||||||||
|
Im Skript “Biegeschwingungen gerader Träger” wird gezeigt, wie für die sehr grobe Einteilung des Trägers in nA = 6 Abschnitte das folgende spezielle symmetrische Eigenwertproblem entsteht:
In
Die 1. Eigenfreuenz nähert den exakten Wert sehr gut, die höheren Frequenzen sind bei dieser groben Diskretisierung erwartungsgemäß recht ungenau. Deshalb wird das Script verallgemeinert, so dass eine beliebig feine Diskretisierung möglich ist.
Im Skript “Biegeschwingungen gerader Träger” wird schließlich noch darauf verwiesen, dass die symmetrische Matrix A Bandstruktur besitzt und die gesamte Information in der Hauptdiagonalen und zwei Nebendiagonalen enthalten ist. Es ist eine wie eine Matlab-Function aufrufbare DLL isiasb_m verfügbar, die die Bandstruktur der beiden Matrizen ausnutzen kann (Speicherplatz und Rechenzeit werden gespart). Die Matrix A wird als symmetrische Bandmatrix folgendermaßen gespeichert:
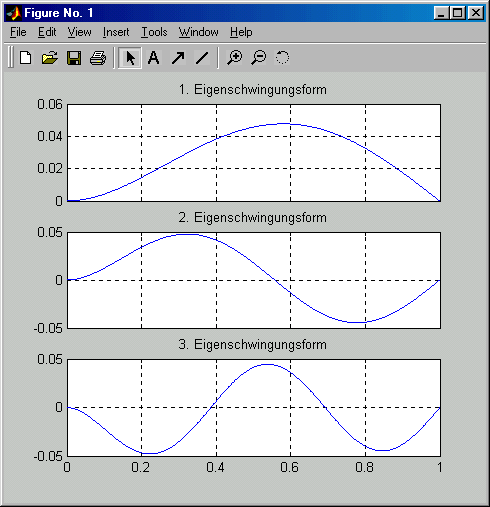
Das nebenstehend zu sehende Matlab-Script realisiert diese Berechnung. Die Matrix A wird als Bandmatrix mit n Zeilen und 3 Spalten aufgebaut, die Matrix B wird mit der Matlab -Function ones (Zeile 14) als Spaltenvektor definiert, der gleichzeitig mit 1-Elemementen gefüllt wird. Der Aufruf (Zeile 24) [nc ev Z] = isiasb_m (A,B,3) ; übergibt die beiden Matrizen und fordert mit der 3 als drittem Parameter die 3 kleinsten Eigenwerte und die zugehörigen Eigenvektoren an. Abgeliefert wird die Anzahl der tatsächlich berechneten Eigenwerte nc, ein Vektor ev mit diesen Eigenwerten und die Matrix Z, die spaltenweise die zugehörigen Eigenvektoren enthält. Die ausführliche Beschreibung der Arbeitsweise und der Anwendungsmöglichkeitender Function isiasb_m (für Interessenten auch der Quellcode) und die für den Aufruf aus Matlab erforderliche DLL findet man unter www.JuergenDankert.de/MatlabFemset. Die von isiasb_m abgelieferten Eigenvektoren werden im Script (Zeilen 28 bis 32) zur graphischen Darstellung der Schwingungsformen genutzt.
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


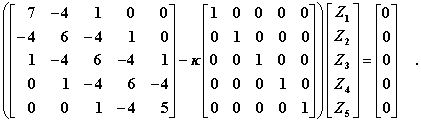
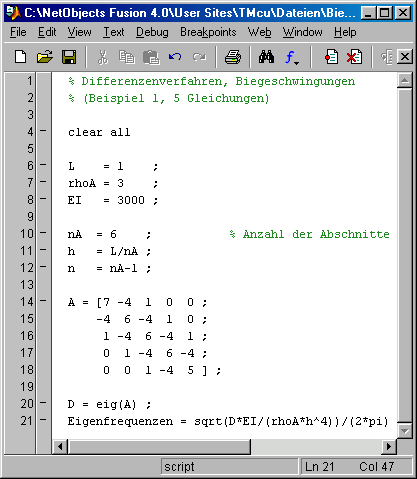 steckt (neben einigen gegebenen Größen) die gesuchte Eigenkreisfrequenz.
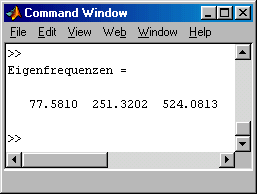
Im nebenstehend zu sehenden Matlab-Script wird das Matrizeneigenwertproblem mit der Matlab-Function eig gelöst. Die berechneten Eigenfrequenzen werden in das Command Window ausgegeben:
steckt (neben einigen gegebenen Größen) die gesuchte Eigenkreisfrequenz.
Im nebenstehend zu sehenden Matlab-Script wird das Matrizeneigenwertproblem mit der Matlab-Function eig gelöst. Die berechneten Eigenfrequenzen werden in das Command Window ausgegeben:
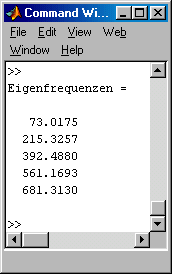
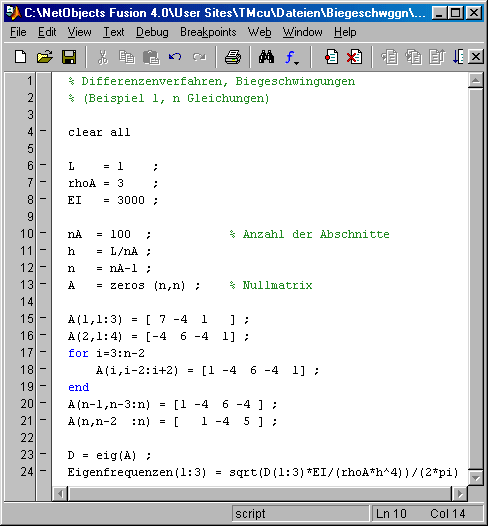 Bei einer feineren Diskretisierung bleiben die von Null
verschiedenen Elemente in den beiden ersten und den beiden letzten Matrixzeilen unverändert, dazwischen ergeben sich weitgehend gleichartige Zeilen (wie die 3. Zeile im oben zu
sehenden Script, jeweils um die Hauptdiagonale angeordnet: 1 –4 6 –4 1). Das nebenstehende Script zeigt den Aufbau des Gleichungssystems für beliebig feine Diskretisierung (zu sehen ist der Fall nA = 100, so dass 99 Gleichungen entstehen. Die
Ergebnisse werden deutlich besser (es werden nur 3 Eigenfrequenzen ausgegeben, obwohl 99 berechnet werden):
Bei einer feineren Diskretisierung bleiben die von Null
verschiedenen Elemente in den beiden ersten und den beiden letzten Matrixzeilen unverändert, dazwischen ergeben sich weitgehend gleichartige Zeilen (wie die 3. Zeile im oben zu
sehenden Script, jeweils um die Hauptdiagonale angeordnet: 1 –4 6 –4 1). Das nebenstehende Script zeigt den Aufbau des Gleichungssystems für beliebig feine Diskretisierung (zu sehen ist der Fall nA = 100, so dass 99 Gleichungen entstehen. Die
Ergebnisse werden deutlich besser (es werden nur 3 Eigenfrequenzen ausgegeben, obwohl 99 berechnet werden):
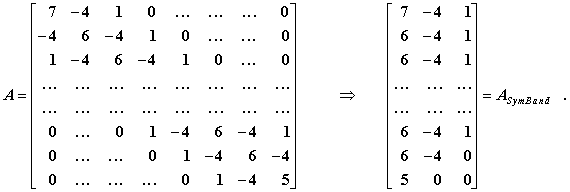
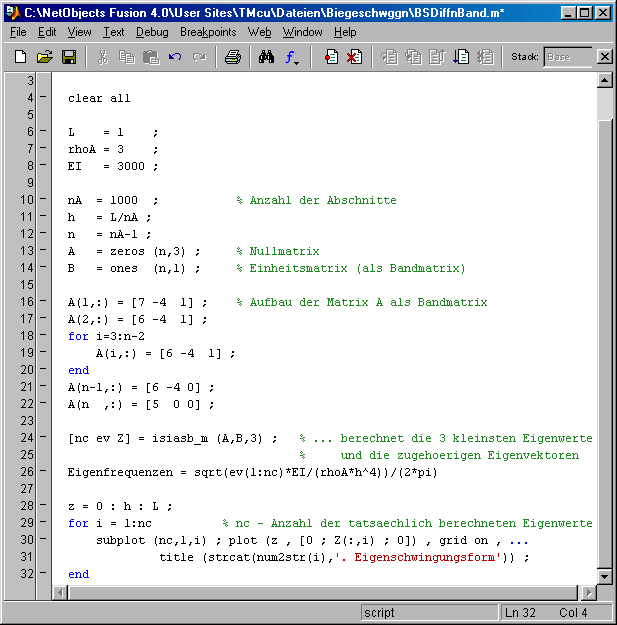 Die Matrix B ist bei einem speziellen
Eigenwertproblem eine Einheitsmatrix, die als Bandmatrix ein Spaltenvektor wird.
Die Matrix B ist bei einem speziellen
Eigenwertproblem eine Einheitsmatrix, die als Bandmatrix ein Spaltenvektor wird.
 Weil durch die Ausnutzung von Symmetrie und Bandstruktur der
Aufwand für die Lösung des Eigenwertproblems drastisch reduziert wird, kann wesentlich feiner diskretisiert werden. Die Einteilung des Trägers in 1000 Abschnitte führt deshalb auf praktisch exakte Ergebnisse:
Weil durch die Ausnutzung von Symmetrie und Bandstruktur der
Aufwand für die Lösung des Eigenwertproblems drastisch reduziert wird, kann wesentlich feiner diskretisiert werden. Die Einteilung des Trägers in 1000 Abschnitte führt deshalb auf praktisch exakte Ergebnisse: