
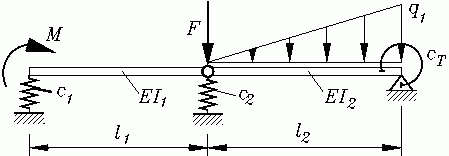
Aufgabe
Für den skizzierten Träger sollen die Biegelinie, der Biegemomentenverlauf und der Querkraftverlauf berechnet werden (Aufgabe aus dem Kapitel "Verformungen durch Biegemomente").
Gegeben:
l1 = 1200 mm ;
EI1 = 2,5 kNm2 ;
c1 = 50 N/mm ;
l2 = 1300 mm ;
EI2 = 5 kNm2 ;
c2 = 250 N/mm ;
cT = 5 kNm ;
q1 = 1,3 N/mm ;
F = 800 N ;
M = 250 Nm .
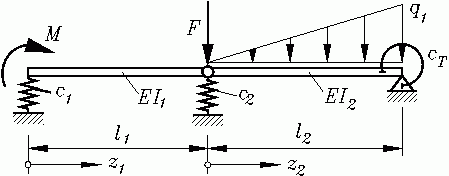
Analytische Lösung
Die Differenzialgleichung der Biegelinie muss für zwei Abschnitte formuliert werden. Mit den nebenstehend zu sehenden Koordinaten gilt:
Viermaliges Integrieren führt auf die beiden allgemeinen Lösungen:
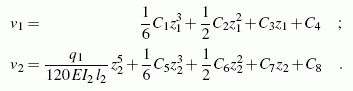
Es sind also 8 Integrationskonstanten zu bestimmen, für die Aussagen über die Verschiebung, die Ableitung der Verschiebung, das Biegemoment und die Querkraft formuliert werden können. Dieser etwas schwierige Part bei der Lösung dieser Aufgabe wird im Kapitel "Verformungen durch Biegemomente" ausführlich beschrieben und führt schließlich auf das folgende lineare Gleichungssystem:
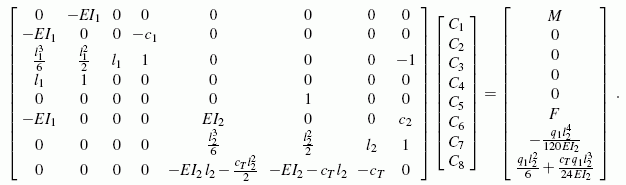
Die Lösung dieses Gleichungssystems ist (mit einiger Mühe) durchaus noch "von Hand" möglich. Weil danach die Auswertung der allgemeinen Lösung mit den dann bekannten Integrationskonstanten aber auch recht aufwendig (und natürlich sehr fehleranfällig) ist, kann dieser Weg kaum empfohlen werden.
Deshalb wird die weitere Rechnung dem nachfolgend gelisteten Matlab-Script übertragen, das das oben zu sehende Gleichungssystem aufbaut, löst und mit den berechneten Integrationskonstanten die Funktionen für die Durchbiegung (entsprechend der oben angegebenen allgemeinen Lösung), das Biegemoment
und die Querkraftverläufe
berechnet, graphisch darstellt und einige spezielle Ergebnisse in das Command Window ausgibt:
clear all
L1 = 1.2 ; % Alle
L2 = 1.3 ; % Werte
EI1 = 2.5 ; % mit den
EI2 = 5 ; % Dimensionen
q1 = 1.3 ; % kN und m
M = 0.25 ;
F = 0.8 ;
c1 = 50 ;
c2 = 250 ;
cT = 5 ;
A = [ 0 -EI1 0 0 0 0 0 0 ;
-EI1 0 0 -c1 0 0 0 0 ;
L1^3/6 L1^2/2 L1 1 0 0 0 -1 ;
L1 1 0 0 0 0 0 0 ;
0 0 0 0 0 1 0 0 ;
-EI1 0 0 0 EI2 0 0 c2 ;
0 0 0 0 L2^3/6 L2^2/2 L2 1 ;
0 0 0 0 -EI2*L2-cT*L2^2/2 -EI2-cT*L2 -cT 0 ] ;
b = [M ; 0 ; 0 ; 0 ; 0 ; F ; -q1*L2^4/(120*EI2) ; q1*L2^2/6+cT*q1*L2^3/(24*EI2)] ;
C = A \ b ;
n = 2500 ; % Anzahl der Abschnitte fuer graphische Darstellung
zi = 0 : (L1+L2)/n : L1+L2 ;
v = zeros(n+1,1) ;
Mb = zeros(n+1,1) ;
FQ = zeros(n+1,1) ;
for i=1:n+1
if zi(i) <= L1
z = zi(i) ;
v(i) = (C(1)*z^3/6+C(2)*z^2/2+C(3)*z+C(4)) ;
Mb(i) = -EI1*(C(1)*z+C(2)) ;
FQ(i) = -EI1*C(1) ;
else
z = zi(i)-L1 ;
v(i) = (q1*z^5/(120*EI2*L2)+C(5)*z^3/6+C(6)*z^2/2+C(7)*z+C(8)) ;
Mb(i) = -EI2*(q1*z^3/(6*EI2*L2)+C(5)*z+C(6)) ;
FQ(i) = -EI2*(q1*z^2/(2*EI2*L2)+C(5)) ;
end
end
subplot (3,1,1) ; plot (zi , v) , grid on , title ('Biegelinie') , axis ij
subplot (3,1,2) ; plot (zi , Mb) , grid on , title ('Biegemoment')
subplot (3,1,3) ; plot (zi , FQ) , grid on , title ('Querkraft')
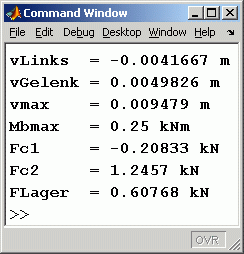
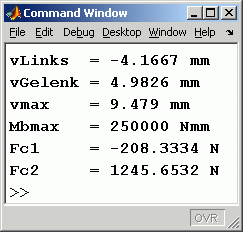
disp (['vLinks = ' , num2str(v(1)), ' m']) ;
disp (['vGelenk = ' , num2str(v(round(n*L1/(L1+L2))+1)), ' m']) ;
disp (['vmax = ' , num2str(max(v)), ' m']) ;
disp (['Mbmax = ' , num2str(max(Mb)), ' kNm']) ;
disp (['Fc1 = ' , num2str(c1*v(1)), ' kN']) ;
disp (['Fc2 = ' , num2str(c2*v(round(n*L1/(L1+L2))+1)), ' kN']) ;
disp (['FLager = ' , num2str(-FQ(n+1)), ' kN']) ;
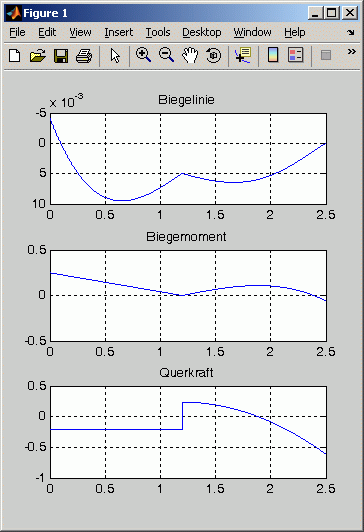
Rechts sieht man die Graphik-Ausgabe des Matlab-Scripts (Biegelinie und Schnittgrößenverläufe).
In das nachstehend zu sehende Command Window wurden einige spezielle Ergebnisse an besonderen Punkten ausgegeben (Absenkung am linken Rand und am Gelenk, maximale Absenkung und maximales Biegemoment, die beiden Federkräfte und die Lagerreaktion am rechten Lager):
Kontrollrechnungen
Die gleiche Aufgabe wurde auch mit dem Differenzenverfahren und mit der Finite-Elemente-Methode gelöst. Klicken auf die nachstehenden Bilder führt zu den entsprechenden Seiten:
 Lösung mit dem Differenzenverfahren |
Lösung interaktiv (www.TM-interaktiv.de) mit der Finite-Elemente-Methode |
